Sommaire :
- Les lignes droites
- D’autres lignes : le cercle et les arcs de cercles
- Longueur et cercle
- Angles
- La symétrie axiale (à venir)
- Triangles et quadrilatères (à venir)
Les fichiers informatiques présents dans cet article sont tous accessibles depuis le site d’activités informatiques de l’IREM Paris Nord : Rubricamaths. L’utilisation de celui-ci permet un accès simple aux activités et permet d’individualiser le travail avec les élèves. En effet, vous y trouverez de nombreuses autres activités similaires à celles présentées avec des niveaux de difficultés graduelles.
Lignes droites : Pour commencer
1. Activité Papier : Figures sur papiers marqués
L’élève doit reproduire le dessin présenté. Il ne peut utiliser comme seul instrument que la règle (non graduée). La seule obligation à respecter est que les points à relier sont des nœuds des papiers maillés, des points des papiers pointés.
On peut moduler le nombre de dessins à proposer en fonction de l’adresse manuelle des élèves, de leur capacité de soin, de leur bonne compréhension des consignes, etc.
La plupart de ces dessins peuvent être proposés comme travail à la maison.
Pour trouver d’autres dessins à réaliser, se reporter aux brochures de l’Irem Paris-Nord, en particulier "Papiers-Crayons". Désormais, les activités monochromes de cette brochure sont disponibles au format pdf. Pour les obtenir, aller à cette rubrique.
2. Activité Géogébra : Découvrir Géogébra
En salle informatique, avec un vidéo-projecteur (si c’est possible), faire découvrir aux élèves :
- les outils de la barre de menu "Lignes droites" : pointer, point, droite, segment, demi-droite, polygone, nommer, cacher/montrer, couleur et remplir ;
- les actions indispensables : déplacer un objet, effacer un objet, etc.
Ensuite, la liste des savoir-faire indispensables est donnée aux élèves qui découvrent et expérimentent à leur rythme ces différentes commandes sur un fichier géogebra vide comprenant uniquement les outils nécessaire.
L’expérience montre que 20 min de découverte et 20 min de libre utilisation sont nécessaires et suffisantes pour la bonne prise en main du logiciel.
Lignes droites : Droites et segments
1. Activité Papier : Reproduire une figure
L’élève doit reproduire le dessin présenté à partir des éléments de départ qui lui sont donnés. Il ne peut utiliser comme seul instrument que la règle ( non graduée). La seule obligation à respecter et qu’aucun des points à relier n’est pris au hasard.
La série suivante de dessin papier est proposée aux élèves :
Les premiers dessins posent parfois de réelles difficultés aux élèves et il faut prendre le soin et le temps de bien leur faire comprendre les consignes. On peut pour cela faire des corrections avec un vidéo-projecteur.
Le coloriage des figures est important pour la suite et doit donc bien être réalisé.
Certains dessins peuvent faire l’objet de travaux à la maison (peut-être après un démarrage en classe).
On peut moduler le nombre de dessins à proposer en fonction de l’adresse manuelle des élèves, de leur capacité de soin, de leur bonne compréhension des consignes, etc.
Pour trouver d’autres dessins, se reporter aux brochures de l’Irem Paris-Nord : "130 Activités mathématiques au collège" et "Papiers-Crayons" . Désormais, les activités monochromes de cette brochure sont disponibles au format pdf. Pour les obtenir, aller à cette rubrique.
2. Activité Géogébra : Reproduire une figure
Vous trouverez sur Rubricamaths de nombreux fichiers dans la partie : Les bases de la géométrie avec Géogebra.
L’élève doit reproduire le dessin présenté à partir des éléments de départ qui lui sont donnés. Pour cela, il utilise les outils du menu "Lignes droites" : point, segment, droite, demi-droite, polygone, couleur, remplir, nommer, cacher/montrer.
Pour certains élèves, il est utile de donner un équivalent papier du travail demandé et d’autoriser ainsi une recherche antérieure ou simultanée avec la règle et le crayon.
La liberté qu’offre Rubricamaths dans le choix des figures proposées aux élèves permet d’individualiser le travail mais doit tout de même suivre une certaine logique.
Voici un exemple de progression :






Shérif et Flash correspondent à l’initiation au travail.
Le choix de refaire Moulinette est volontaire. Il doit permettre à l’élève de bien comprendre que les points nécessaires à la réalisation des polygones attendus sont des points d’intersection de lignes (segments) qui relient des points déjà existants. Ce premier dessin peut être "assisté" en utilisant un vidéo-projecteur et en faisant voir, par un élève, au groupe comment obtenir un ou des sommets des ailes du moulin. On peut proposer une autre figure du même genre pour vérifier l’acquisition de ce principe.
La réalisation de tous ces dessins nécessite le tracé de lignes droites. Si les trois premiers dessins n’utilisent que l’outil "segment", il n’en va pas de même avec Hextoile qui va exiger l’emploi de l’outil "demi-droite" et Multiflash l’usage de l’outil "droite".
Le dernier dessin "Soissons" n’est là que pour les "experts", ceux qui, allant plus vite, finissent très rapidement les premières figures.
3. Bilan
Notions rencontrées : point, droite, segment, demi-droite.
Vocabulaire complémentaire : extrémités d’un segment, origine d’une demi-droite, points alignés.
Après les activités proposées, l’élève doit avoir compris la différence entre droite, demi-droite et segment. Il pourra exprimer (voire noter sur un cahier) ces différences en termes naïfs (qu’il n’est peut être pas utile de corriger). Il lui faut aussi retenir les mots de vocabulaire utilisés. On peut aussi lui faire comprendre que pour écrire symboliquement "la doite passant par A et par B" ou "le segment d’extrémités A et B" il va être nécessaire de différencier par un code l’arrêt (extrémités, origine) du non-arrêt de la ligne. Les élèves ne manquent pas d’imagination pour marquer cette différence ( ... et / par exemple). Il ne restera plus alors qu’à donner le code commun en expliquant ce qu’est une convention et à quoi elle sert.
Lignes droites : Droites perpendiculaires
Les activités informatiques de cette partie sont accessibles sur Rubricamaths en suivant ce lien.
1. Géométrie mentale avec Géogebra : Trou
L’activité "Trou" se trouve à l’endroit indiqué précédemment.
On commence en présentant aux élèves le processus illustré ci-dessous :
Puis, on propose aux élèves de faire des séries de 10 essais jusqu’à l’obtention d’un score supérieur à 18.
L’expérience montre qu’à condition d’être patient la très grande majorité des élèves acquièrent une incroyable précision dans le positionnement du "trou" et c’est tout l’intérêt de cette activité.
2. Géométrie mentale avec Géogebra : perpendiculaires
L’activité "Perpendiculaires" se trouve à l’endroit indiqué précédemment.
La situation de départ est la même que la précédente mais cette fois c’est la perpendiculaire à la droite qu’il faut tracer. Il faut là encore que les élèves obtiennent le plus haut score possible avec des séries de 10 essais.
Il n’est guère besoin de recommencer de nombreuses fois, les résultats obtenus sont très souvent excellents assez rapidement.
3. Bilan :
Notions rencontrées : droites perpendiculaires
Après les activités proposées, l’élève est capable de tracer empiriquement sur l’écran de l’ordinateur la perpendiculaire à une droite donnée passant par un point donné. Il est nécessaire de rappeler à ce moment le mot "perpendiculaire". Une définition au sens propre n’est pas nécessaire, le processus de tracé approximatif suffit pour l’instant.
On peut/doit aussi montrer qu’un double pliage d’une feuille de papier permet d’obtenir deux plis perpendiculaires (serait-ce une définition possible ?).
4. Activité Papier :
L’activité suivante permet la transition sur papier. Le papier marqué (pointé ou quadrillé) reste un support privilégié pour le tracé. Les élèves doivent arriver à formuler oralement une méthode permettant de tracer la perpendiculaire à une droite donnée passant par un point donné dans les situations proposées.
La réponse attendue devrait ressembler à quelque chose comme : en comptant des carrés, pour le segment rouge 3 à droite et 2 en bas ; pour le segment vert 2 à droite et 3 en haut.

5. Procédure :
Il est temps de montrer aux élèves comment tracer une perpendiculaire à une droite donnée passant par un point donné avec une règle et une équerre. Mais tout sera très aisé car ils savent déjà où se placera cette droite.
La feuille ci-contre servira d’aide mémoire :
6. Réinvestissement :
Pour terminer cette leçon, proposons aux élèves plusieurs activités de dessin (extraites du "Carnet de stage 3").
Lignes droites : Droites parallèles
1. Activité Géogébra : en classe
Cette introduction est réalisée avec un vidéo-projecteur devant la classe.
On trace une droite (D), on place deux points A et B sur cette droite et les droites perpendiculaires à (D) passant par A et B.
On fait observer la position des droites après avoir fait tourner (D) autour du point qui a servi à la créer. On peut utiliser avec précaution l’outil Géogébra "Relation entre deux objet" qui permettra de trouver qu’elles sont parallèles.
Cette observation doit permettre un débat en classe : quelle est la signification de cette notion de parallèles ? On privilégiera l’absence de point d’intersection à la notion d’écart constant qui est bien souvent celle proposée.
Notions rencontrées : droites parallèles
L’élève doit pouvoir formuler : "Deux droites perpendiculaires à une même troisième droite sont parallèles".
2. Activités Papier
a) L’ activité ci-contre joue le même rôle transitoire que son équivalent dans la partie précédente. Comme c’est encore plus simple que de tracer des perpendiculaires, nul n’est besoin d’insister.
b) On doit aussi proposer de tracer une parallèle à une droite (d) donnée passant par un point M donné, sur papier blanc.
Le procédé employé va, bien entendu, consister à tracer la perpendiculaire (d’) à (d) passant par M puis la perpendiculaire à (d’) passant par M (la formulation correcte, en français, du processus est sans doute utile).
3. Procédure
Montrons maintenant aux élèves comment tracer plus efficacement une parallèle à une droite donnée passant par un point donné avec une règle et une équerre.
La seule chose qui reste à faire est de montrer qu’il n’est pas utile de tracer physiquement la droite (d’) précédemment utilisée, le positionnement de la règle remplacera ce tracé.
La feuille ci-contre servira d’aide mémoire :
4. Activités Papier
Pour utiliser la procédure précédente, nous pouvons proposer aux élèves quatre activités de dessin.
D’autres dessins utilisant des tracés de parallèles peuvent être proposées.
L’idée des ombres peut être reprise, étendue,etc. Son côté "vie-courante" plaît bien aux élèves.
Les dessins ci-dessus sont extraits de "Carnet de stage 3" où vous pourrez trouver d’autres propositions de tracés.
5. Activité Géogébra :
Cette activité est réalisée avec un vidéo-projecteur devant la classe.
On trace deux droites parallèles (D) et (D’) puis (D") une parallèle à (D’). Qu’observe-t on ? On peut utiliser l’outil "Relation entre deux objet".
On trace deux droites parallèles (D) et (D’) puis (D") une perpendiculaire à (D’). Qu’observe-t on ? On peut utiliser l’outil "Relation entre deux objet".
Dans les deux cas, les élèves doivent s’exprimer pour qu’on arrive à :
"Deux droites parallèles à une même troisième droite sont parallèles sont parallèles entre elles "
" Si deux droites sont parallèles, toute perpendiculaire à l’une est perpendiculaire à l’autre"
D’autres lignes : le cercle
1. Activité collective :
L’objectif de cette activité est de faire percevoir aux élèves qu’un cercle est l’ensemble des points situés à une même distance du centre.
L’activité se déroule au tableau ou au vidéo-projecteur. On trace un point A et on demande à un élève volontaire de tracer un point situé à 40 cm de A sans, bien sur, préciser quels sont les outils à utiliser. On demande la même chose à un deuxième élève, puis un troisième, ....
L’étape suivante consiste à demander combien on peut tracer de tels points ( c’est toujours intéressant et parfois surprenant) puis ce qu’on peut dire de la position de tous ces points.
Une fois le cercle tracé, il ne faut pas manquer de vérifier qu’un point quelconque du cercle est bien, lui aussi, placé à la distance voulue du centre. Les mots "cercle" et "rayon" sont alors définis.
Notions rencontrées : cercle, rayon d’un cercle
2. Activités papier :
Afin de s’assurer de la bonne maîtrise du compas par les élèves dans le domaine du tracé de cercle, nous pouvons leurs proposer des algorithmes de construction. Ils ont l’avantage de faire tracer de très nombreux cercles et d’être la plupart du temps assez motivant, la figure finale n’apparaissant clairement que lorsqu’elle est terminée.
Pour commencer, nous pouvons leur proposer cet algorithme :
- Tracer une droite.
- Placer sur cette droite une vingtaine de points.
- Choisir un point.
- Tracer le cercle ayant pour centre le point choisi et ayant pour rayon 2 cm.
- Recommencer pour chacun des points.
La construction est visualisable en suivant ce lien (déplacer le point rouge).
Ensuite, nous pouvons leur proposer ces deux algorithmes. les deux versions correspondent à la forme de l’énoncé : dans la version 1, l’énoncé prend la forme de vignettes illustrant la construction alors que dans la version 2, l’énoncé prend la forme d’un programme de construction.
L’enveloppe de cercle n°1 correspond à un limaçon de Pascal, on peut obtenir une cardioïde à condition de mettre le point extérieur sur le cercle. Vous pouvez visualiser la construction en suivant ce lien (le point bleu peut se déplacer).
L’enveloppe de cercle n°2 est visualisable en suivant ce lien (déplacer le point rouge)
3. Activités papier :
Nous pouvons aussi proposer quelques figures à reproduire construites uniquement avec des cercles.
D’autres lignes : les arcs de cercles
Quelques dessins à réaliser vont permettre aux élèves de se perfectionner dans l’utilisation du compas et leur permettre d’appréhender le tracé d’arcs de cercle.
D’autres dessins sont disponibles dans "Carnet de stage 4" et dans"Papiers-Crayons".
De plus, il peut être intéressant de travailler sur des activités informatiques. On peut en trouver sur Rubricamaths dans la partie Des cercle et des arcs de cercles, notamment des activités de géométrie mentale.
Longueur et cercle : Comparer, reporter, reproduire
1. Activités Papier :
Les deux activités proposées ci-contre ont pour objectif de montrer le rôle du compas dans la comparaison des longueurs de segments ; d’abord on compare les segments deux à deux (par référence à un modèle) ensuite on classe entièrement une famille de segments par comparaisons multiples. Cette deuxième activité est l’occasion de faire énoncer en français un "algorithme" de classement total à partir d’une comparaison deux à deux.
2. Activités Papier :
On complète l’idée de comparaison mise en place précédemment, en comparant cette fois des lignes. Le dernier cas permet de définir le périmètre d’une figure comme étant la longueur de la ligne fermée qui la compose.
Les trois activités précédentes sont extraites de "130 Activités" :
3. Procédures :
Il faut maintenant apprendre aux élèves à reproduire à l’identique (*) des figures géométriques. Cette activité est d’une grande importance pour toutes les leçons à suivre et sera donc traitée avec le plus grand soin.
(*) l’idée de " à l’identique" est matérialisée par l’usage du calque qu’on peut bien sur déplacer, tourner voire retourner.
Chaque élève travaille sur une feuille de papier blanc et doit reproduire les figures proposées sur la feuille ci-contre.
Chaque étape est corrigée.
La première figure, un arc et son centre, pose tout de suite un problème difficile : comment faire pour que la longueur de l’arc soit la bonne ? L’idée d’utiliser la corde qui sous-tend cet arc est loin d’être naturelle (bien que toujours trouvée par au moins un élève) aussi faut-il s’assurer (avec un papier calque) que la méthode fonctionne bien.
La deuxième figure, un secteur, permet de vérifier que la première construction est comprise et introduis la figure suivante.
Reproduire un angle est une étape importante pour la suite ; la reproduction précédente amène le plus souvent une réponse rapide.
Arriver à reproduire un triangle peut découler des tracés antérieurs.
Reproduire un polygone par "triangulation" vient aussi assez naturellement.
La bonne maîtrise de cette technique étant indispensable, il paraît souvent utile de proposer d’autres activités du même type.
Longueur et cercle : Médiatrice d’un segment
1. Activités Geogebra :
Pour commencer cette activité, il faut ouvrir le fichier Geogebra « Pour découvrir » disponible dans la partie médiatrice d’un segment de Rubricamaths .
Sur l’écran s’affiche un segment ; une de ces extrémités est colorée en rouge l’autre en vert. De nombreux points parsèment l’ écran. Il est demandé à l’ élève (voir fiche "consignes" ci-contre) de colorer ces points en rouge si ils sont plus près de l’ extrémité rouge que de l’ extrémité verte, en vert si c’est l’inverse. Nous attendons que les élèves utilisent (en cas de doute seulement ?) l’outil "Cercle".
Bien sur, quelques points sont situés à égale distance des deux extrémités. Après ce constat, il est demandé aux élèves d’émettre une conjecture quant à la position de ces points (alignement) puis de tracer la ligne qui les regroupe, de vérifier que n’importe quel point de cette ligne est bien situé à égale distance des extrémités du segment (en traçant un cercle centré en ce point et passant par une extrémité, on constate que le cercle passe aussi par l’autre extrémité même quand on déplace ce point sur la droite).
Il reste à observer puis vérifier les propriétés de cette droite (perpendiculaire au segment et passant par le milieu).
Pour terminer, on demande aux élèves de tracer un segment, de tracer la perpendiculaire passant par le milieu du segment et de vérifier que n’importe quel point de cette droite est situé à la même distance des deux extrémités.
Notions rencontrées : médiatrice d’un segment, milieu d’un segment.
2. Procédures :
Le passage sur papier est à faire maintenant. On peut demander aux élèves de tracer la médiatrice d’un segment à l’aide d’une règle non graduée et d’un compas ; les procédures envisagées ont souvent besoin d’être légèrement simplifiées pour arriver à celle présentée ci-contre. Le document est fourni aux élèves et servira d’aide-mémoire. ".
On pourra aussi faire énoncer/noter une définition et une propriété caractéristique de la médiatrice.
3. Activités Papier :
Deux activités vont permettre la mise en place de la notion. La troisième est un exercice de recherche pour les élèves les plus avancés.
Longueur et cercle : Mesurer une longueur
1. Activités Papier :
L’objectif de ces deux activités est de faire comprendre la non-universalité des unités de mesure.
Il existe des systèmes de mesure de longueur différents de celui que nous utilisons (on peut en faire chercher d’autres, sur le net par exemple).
On pourra faire remarquer qu’un changement d’unité ne modifie pas la forme de la figure mais seulement sa taille.
Notions rencontrées : unité de mesure de longueur
2. Procédures :
Il est sans doute utile à ce moment de faire rappeler par les élèves le fonctionnement du système métrique avec son unité principale, ses multiples et sous-multiples.
L’activité ci-contre permettra à la fois de s’exercer sur les conversions mais aussi de travailler sur les ordres de grandeur.
On peut aussi faire évaluer puis mesurer des longueurs ( largeur et longueur de la salle de classe, du tableau, des tables, du couloir,...).
Notions rencontrées : le mètre, multiples et sous-multiples
3. Activités Papier :
Pour terminer cette leçon, on peut proposer quelques exercices de tracés :
- tracer des triangles connaissant les longueurs de leurs côtés ;
- tracer tous les triangles de périmètre 15 cm et dont les côtés ont pour longueur des nombres entiers de centimètres ;
- tracer sur papier à petits carreaux (pour éviter le tracé approximatif des angles droits) un carré connaissant la mesure de son périmètre, ou d’un rectangle connaissant son périmètre et la longueur d’un côté.
- .....
Longueur et cercle : Cercles et arcs de cercle
1. Procédures :
Des procédures qu’on peut découvrir ensemble : partager un cercle en 2, 3, 4, 5, 6, 8, 10 et 12 parts égales. Ce travail peut se faire en plusieurs (3 ?) fois et être illustré, dans chaque cas d’un dessin à réaliser.
Ces constructions assez complexes mettent en œuvre l’utilisation de la médiatrice (ou de la bissectrice si elle a déjà été étudiée) pour trouver des points équidistants et ainsi doubler le nombre de points sur le cercle.
Ces programme de construction sont à faire avec les élèves à l’aide d’un vidéo-projecteur. Ne pas oublier de valider au compas ces différentes constructions. Les élèves admettent (volontiers) que si, dans un même cercle, des cordes ont la même longueur alors les arcs correspondant aussi.
2. Activités Papier :
Pour se mettre en tête les procédures ci-dessus, nous proposons quelques dessins à réaliser.
Problèmes de construction
1. Activités géogebra : Programmes de construction
Les activités informatiques de cette partie sont accessibles sur Rubricamaths en suivant ce lien.
Afin de mettre en œuvre les objets mathématiques utilisés jusqu’à présent dans le cadre de la construction d’une figure, nous proposons aux élèves les activités informatiques suivantes :




Pour cette série, l’élève doit construire les figures, vérifier leur validité en déplaçant les points libres puis écrire sur papier la suite d’instruction qui permet sa construction.
Ce travail permet de travailler l’ordre de construction de la figure et la notion de points libres (point bleu) et de points liés (point noir). Il permet, de plus, de dissocier la construction du texte à produire, celui-ci n’étant à réaliser qu’après la validation de la figure.
2. Activités géogebra : Problèmes de construction
Les activités informatiques de cette partie sont accessibles sur Rubricamaths en suivant ce lien.













L’objectif unique de ces activités est la construction de figure. Il n’est plus demandé de produire un texte. Les 6 premières activités sont issues de la même situation géométrique mais les conditions de départ varient ainsi que les outils mis à la disposition des élèves pour réaliser la construction. De la même manière que précédemment, les élèves peuvent vérifier la validité de leur construction en déplaçant les points de départ.
Les activités suivantes proposent des constructions toujours différentes avec des outils limités.
Angles : Comparer, reporter, reproduire
1. Activités Papier :
Comme nous l’avons fait pour les longueurs, la première chose à faire pour les angles est de savoir les comparer. Aussi commencerons-nous par une activité suggérant l’utilisation du compas pour réaliser des comparaisons.
Avant de commencer il ne sera peut-être pas inutile de reprendre (au tableau ou au vidéoprojecteur) la reproduction d’un angle à l’aide d’un compas.
2. Activités Papier :
Les élèves connaissent et ont revu (voir ci-dessus) comment reproduire un angle à l’aide d’un compas. Nous allons utiliser ce savoir faire pour réaliser une liaison avec la leçon précédente (partage du cercle).
Angles : Logo 1
1. Introduction :
Pour des raisons pratiques cette leçon est placée dans ce chapitre mais il paraît possible que, dans le temps, elle soit située bien avant. Rien n’empêche de commencer à utiliser Logo en classe de sixième très tôt dans l’année.
Nous invitons les enseignants qui connaissent mal (ou pas) Logo à consulter les quelques pages d’introduction situées dans la partie dédiée de ce site puis à charger une version gratuite de Logo.
Le logiciel qui a été développé au sein de l’IREM PARIS NORD se nomme GeoTortue mais d’autres LOGO sont disponibles sur le net : Cliquer sur ce lien pour accéder à l’espace GeoTortue de ce site
Il est aussi possible de réaliser ces activités avec d’autres logiciels, par exemple Scratch ou DGPad qui sont des langages utilisant des blocs.
2. Logo : pour commencer
C’est le premier contact avec le langage Logo , il a une importance considérable puisqu’il va conditionner toute la suite. L’élève doit se familiariser avec l’environnement qu’il découvre.
Il paraît donc important de bien observer ce que font les élèves et d’adopter le rythme de travail qui convient à chacun.
La démarche proposée ici n’est qu’indicative et chacun l’adaptera à ses propres sensibilités, à ses propres élèves. Toutefois, cette démarche a été expérimentée dans plusieurs établissements et elle a monté qu’elle était applicable par tous.
– Première étape :
Avec un vidéoprojecteur (?) ou individuellement, montrer les actions produites par les quatre ordres : AV, RE, TD, TG .
Il nous semble préférable d’effectuer ces actions crayon levé.
– Deuxième étape :
Laisser les élèves jouer avec ces instructions le temps nécessaire (?) à leur bonne compréhension.
– Toisième étape :
Demander individuellement à l’élève d’atteindre avec la tortue un point précis de l’écran ( un coin ou un emplacement matérialisé par un bout de post-it ou un morceau de pâte à coller ).
– Quatrième étape :
Montrer que la tortue peut laisser une trace derrière elle (BC) et demander la réalisation d’un circuit (un huit autour de deux points matérialisés de l’écran par exemple).
Profiter d’une erreur pour montrer le rôle de l’ordre : VG.
Des activités complémentaires de découvertes sont disponibles sur Rubricamaths dans la partie Les bases de la géométrie avec GéoTortue, pour commencer.
3. Logo : Angles de base
Cette première activité a pour objectif de faire découvrir aux élèves que la valeur 90 joue un rôle privilégié dans les rotations de la tortue.
Pour des élèves connaissant la mesure des angles en degrés, cette découverte est rapide et sans surprise mais pour les autres, elle ne se fera qu’après de nombreux essais-erreurs. Les erreurs apparaissent nettement à l’écran dès le premier dessin (traits "en échelle"), il n’est donc pas nécessaire d’insister beaucoup pour indiquer à l’élève le succès ou l’échec de ses tentatives. Petit à petit, il prendra ainsi l’habitude d’évaluer seul sa propre production.
Les deux derniers dessins proposés incitent à partager un angle droit en deux puis en trois parties égales
Angles : Logo 2
1. Logo : Carrés
Cette activité introduit la notion de procédure, indispensable pour la suite.
Pour les élèves ayant assimilé la notion d’angle droit, faire tracer par la tortue un carré ne va pas présenter une difficulté majeure. Seul, peut-être l’orientation de la tortue sera encore source de problèmes chez certains.
Une fois le dessin achevé, il suffira à l’enseignant de montrer qu’on peut "apprendre" à la tortue à le réaliser directement. L’idée de procédure comme moyen d’apprendre de nouvelles instructions à la tortue passe naturellement.
L’étape suivante est importante. Il faut faire comprendre aux élèves qu’une procédure peut/doit être réutilisée pour réaliser un dessin plus complexe. Il faudrait être intraitable avec les élèves qui n’utilisent pas la procédure "Carré" pour tracer "Drapeau" , "Panneau" ou "Doublecarré" et leur faire recommencer le dessin jusqu’à ce qu’il utilise "Carré". Pour justifier cette exigence, le moindre nombre d’instructions peut être une raison acceptée.
2. Logo : Triangles
Cette fiche doit faire avancer les élèves dans la compréhension de la notion de procédure et les conforter dans la maîtrise des valeurs angulaires.
La recherche de la procédure "triangle" permet d’installer une méthode de recherche. Pour trouver la bonne valeur de l’angle de rotation on peut/doit procéder par essais-erreurs. Une valeur trop grande fera se croiser les côtés alors qu’une valeur trop petite ne permettra pas la fermeture de la figure. L’élève pourra évaluer seul le résultat de son travail. Attention à ceux qui, ayant des connaissances préalables, sont surpris que la valeur 60 ne soit pas la bonne. La distinction entre angle intérieur et angle extérieur, qui n’apparaissait pas avec les carrés, est à faire. Notre brave tortue se préoccupe beaucoup plus des angles extérieurs des polygones que la géométrie plus classique de collège ne le fait.
Avec des gabarits
Nous avons constaté par expérience que de nombreux élèves avait des difficultés à maîtriser l’usage du rapporteur. Les raisons sont multiples mais on peut néanmoins en dégager quelques unes :
- L’outil lui-même qui lorsqu’il prend la forme d’un demi-disque avec deux graduations n’est pas simple pour débuter.
- Des images mentales peu claires que se font les élèves d’un angle : confusion entre l’angle et sa mesure, confusion avec les longueurs.
- Les nombreuses compétences que l’on demande aux élèves d’assimiler en même temps que l’apprentissage de l’utilisation du rapporteur (repérer un angle dans une figure complexe, reproduire des figures en particulier les triangles...).
Ainsi, il nous paraît pertinent de commencer par travailler les angles avec des gabarits. Cela permettra à l’élève de travailler les différentes compétences sur les angles sans être en surcharge à cause de l’utilisation du rapporteur et ainsi de consolider d’abord les images mentales qu’il s’en fait.
1. Partage de l’angle de 360° et construction des gabarits
Dans partie inférieure de la feuille, il faut déterminer la mesure de l’ensemble des angles par partage de 360°, par addition ou soustraction d’angles. Après correction, chaque secteur angulaire est découpé soigneusement et rangé dans une pochette plastique. Ces gabarits seront les outils pour la suite des activités.
Nous disposons des angles de : 15° ; 18° ; 20° ; 30° ; 40° ; 45° ; 50° ; 60° ; 70° ; 72° ; 90° ; 110° ; 120°
2. Mesurer, comparer des angles
- Ranger les angles dans l’ordre croissant à l’œil (sans utiliser ni gabarit, ni rapporteur)
- Trouver tous les angles qui mesure 40° en utilisant un gabarit
- Encadrer chacun des angles en utilisant des gabarits
- Ranger de nouveau les angles dans l’ordre croissant.
Quelques commentaires :
question 1) et question 2) : l’idée est de forcer les élèves à évaluer les angles avant de manipuler les gabarits et surtout de casser certaines représentations erronées que peuvent avoir les élèves sur les angles. Bien des élèves classeront les angles selon leur taille (la place prise sur la feuille) et non selon leur ouverture. Les angles a et f mesurant tout deux 40° permettent de mettre en évidence cette erreur.
question 3) et 4) : l’objectif est double :
- permettre aux élèves de placer correctement le gabarit sur l’angle (alignement des centres, alignement des côtés).
- évaluer la mesure d’un angle
- ranger les angles par comparaisons successives.
Cette fiche pourra servir de nouveau plus tard quand il sera question de mesurer avec un rapporteur.
3. Repérer, nommer, mesurer un angle
- mesurer les angles à l’aide de gabarit,
- repérer certains angles dans une figure complexe,
- maîtriser la notation d’un angle avec trois lettres.
Une version de l’activité au format A4 est téléchargeable en suivant ce lien.
4. Construire un angle, reproduire une figure
La plupart des angles donnés ne sont pas présents dans les gabarits. Il faut donc que les élèves obtiennent les angles par addition ou soustraction de deux angles (45°-20°=25° ; 180°+40°=220° ; 360°-40° = 320°, ...).
Ensuite, il leur faudra construire des triangles et des figures plus complexes.
Une version de l’activité au format A4 est téléchargeable en suivant ce lien.
5. Recherche : Le billard /1
La réponse à la question posée dépend fortement de la précision et du soin que l’élève a apporté à ses tracés.
On peut aisément leur faire constater la présence de parallèles après quelques rebonds. Ils auront alors la possibilité de terminer leur tracé avec la règle et l’équerre.
Voici quelques travaux d’élèves (suivre ce lien) qui permettent de se rendre compte du résultat final et de constater la répercussion d’une erreur ou d’un manque de précision sur l’ensemble :
– travaux 1 et 2 : bonnes solutions avec de légères différences de trajets dues à l’imprécision des mesures (imprécision tout à fait acceptable)
– travaux 3 et 4 : solutions presque correctes avec seulement une trajectoire incorrecte
– travaux 5, 6 et 7 : solutions avec deux trajectoires incorrectes.
Une simulation de cette activité avec GéoTortue est disponible en suivant ce lien (il faut avoir installé au préalable GéoTortue). Elle peut être utilisée pour faire un bilan collectif.
Avec un rapporteur
Dans la partie précédente, les élèves ont repéré et nommé des angles, les ont mesurés, les ont construits, ont reproduit des figures (des triangles en particulier) avec des gabarits. Les élèves ont donc acquis les différentes compétences qui concernent les angles et commencent à en avoir de bonnes images mentales.
Dans cette partie, nous allons faire le point sur les différents types d’angles et nous concentrer sur l’utilisation du rapporteur. Nous reprendrons ensuite la même démarche que précédemment. Nous complexifierons progressivement les constructions en particulier en proposant des programmes de construction à base de texte.
1. Les différents types d’angles
- angle saillants (entre 0° et 180°)
- angle nul (O°)
- angle aigu (entre 0° et 90°)
- angle droit (90°)
- angle obtus (entre 90° et 180°)
- angle plat (180°)
- angle rentrant (entre 180° et 360°)
Ci-contre, la partie de la leçon correspondante tirée d’un cahier d’élève.
Ensuite, une présentation de rapporteurs (circulaire ou semi-circulaire) est réalisée. Il s’agit de montrer comment les utiliser pour mesurer et construire des angles.
2. Evaluer un angle en degré
Ces deux activités nécessitent d’évaluer les angles en les comparant avec des fractions d’angles bien connus (45° ; 90° ; 180° ; ...). Après quelques séances de 10 minutes chacune, les progrès des élèves sont assez flagrants.
3. Repérer, nommer, mesurer un angle avec un rapporteur
- mesurer les angles à l’aide d’un rapporteur,
- repérer certains angles dans une figure complexe,
- maîtriser la notation d’un angle avec trois lettres.
Une version de l’activité au format A4 est téléchargeable en suivant ce lien.
4. Construire un angle, reproduire une figure avec un rapporteur
La précision est quant à elle évaluée sous la forme d’une cible. Le point final ne se trouve pas au centre de celle-ci, cela autoriserait trop les élèves à des ajustements. De plus, la position de ce point dépend du redimensionnement effectué lors de l’impression de cette feuille.
5. Construire un angle, construire une figure avec un rapporteur
C’est globalement le même principe que l’activité précédente sauf que les consignes ne sont pas totalement visuelles mais données sous la forme d’un texte. De plus, la consigne est plus complexe (il faut comprendre ce qu’est un zigzag) et la construction est plus longue. Elle demande donc davantage de précision. Les cibles sont présentes pour évaluer la précision de la construction.
Si des élèves sont en avance, nous pouvons leur proposer de créer leur propre zigzag. Ils devront pour cela imaginer une construction puis produire un texte de consignes à destination ce qui est très formateur. Nous pouvons ensuite proposer aux élèves de se regrouper par deux, chacun proposant alternativement son zigzag à l’oral à l’autre qui le réalise.
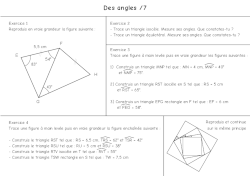
6. Autour des triangles
7. Recherche : Pi piquant /1
Pour cela, il pourra s’appuyer sur plusieurs documents :
- Des photos de certains des tableaux de François Morellet (suivre ce lien). Ils peuvent être utiles pour montrer que ce sont des œuvres réelles et concrètes, pour illustrer le principe de construction ainsi que les différentes possibilités de création.
- Une simulation de cette activité avec GéoTortue (suivre ce lien) ou avec Snap ! (suivre ce lien qui fonctionne directement en ligne). Cette simulation peut être utilisée pour faire comprendre le principe, faire varier les différents paramètres et permettre aux élèves de visualiser le résultat final avant de réaliser leur construction.
Le fichier GéoTortue nécessite que ce logiciel soit installé préalablement sur l’ordinateur.