Le fichier Géogebra 3D (à partir de la version 5) suivant est proposé aux élèves.
Ils ne peuvent que manipuler l’espace graphique, déplacer les points verts qui déterminent le plan de coupe et éventuellement placer des milieux qui serviront de repère.
Cliquer sur l’image suivante pour obtenir le fichier ou passer par Rubricamaths->rubrique71]
La consigne donnée aux élèves pour cette activité est de déplacer les points verts pour obtenir les figures suivantes :
- un hexagone
- un hexagone régulier
- un pentagone
- un carré
- un rectangle
- un triangle équilatéral
- un triangle isocèle
- un triangle rectangle (impossible)
- un triangle quelconque
- un trapèze isocèle
- un parallélogramme
- un losange
- un quadrilatère quelconque (impossible)
- un heptagone (impossible)
pour les élèves les plus avancés :
- un pentagone régulier (impossible)
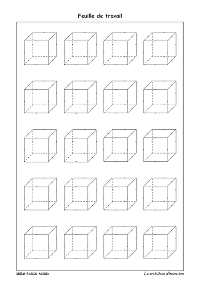
Les élèves devront reproduire chacune de ses figures sur la feuille de travail suivante composée de cubes représentés en perspective (les milieux des arêtes sont présents pour faciliter les tracés) :
L’objectif de cette activité est double :
- faire manipuler l’espace graphique 3D par les élèves.
- leur faire découvrir les sections du cube et plus généralement les caractéristiques des sections de solides.
En effet, les questionnements sur les égalités de longueurs nécessaires pour réaliser les différentes sections du cube mèneront inévitablement les élèves à observer le solide dans des vues planes bien choisies (nous pourrons les guider dans ce sens s’ils ne le font pas d’eux-mêmes).
De plus, ils réaliseront intuitivement que les côtés d’une section sont obligatoirement des segments d’une des faces du cube, ce qui est un enjeu majeur dans l’étude des sections de solides. D’ailleurs, le choix de proposer un heptagone impossible à construire est délibéré car il confronte l’élève à cette caractéristique des sections et l’oblige pour comprendre à un raisonnement du type : "le cube a 6 faces et le polygone doit avoir tous ses côtés dans une des faces du cube donc le polygone ne peut avoir qu’un maximum de 6 côtés".
Concernant le quadrilatère quelconque, l’idée est la même que précédemment. Il est impossible de le construire car il y a obligatoirement deux côtés opposés du quadrilatère qui se situent dans deux faces opposées du cube et donc qui sont parallèles.
Quant au pentagone régulier, il est impossible de le réaliser car chacun de ses angles devraient mesurer 108° et qu’il y a au moins un angle de la section pentagonale qui est plus petit que 90°.
Voici quelques aperçus de ce que l’on peut observer en utilisant ce fichier :