Dans l’activité suivante, le support est uniquement informatique sous la forme d’un fichier Geogebra (dans sa version 5).
Les élèves devront produire un compte-rendu de ce qu’ils ont observé, manipulé et constaté.

Les consignes suivent trois phases :

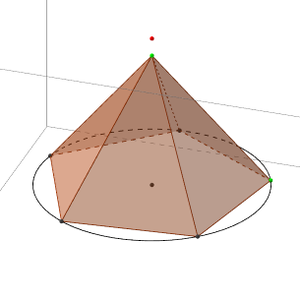
• Observer/décrire les pyramides en manipulant les points colorés verts et oranges.
• Utiliser l’outil "lier/libérer un point" pour pouvoir déplacer le sommet de la pyramide dans n’importe quel sens. Déplacer les points et observer/décrire.
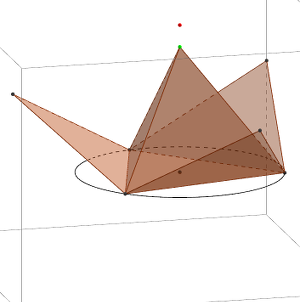
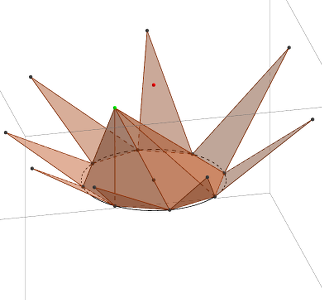
• Faire apparaître le patron en cochant la case, un nouveau curseur apparaît. Déplacer les points puis observer/décrire.
• Observer/décrire la section d’une pyramide en déplaçant le point rouge.

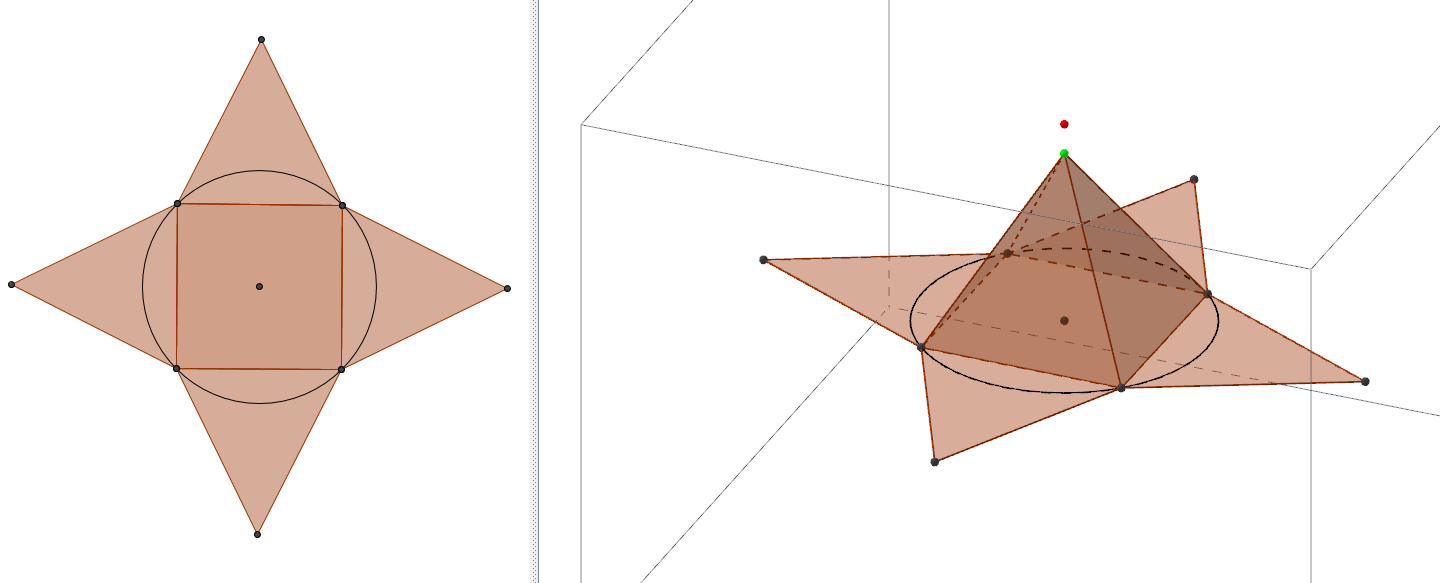
Voici quelques captures d’écran de ce que l’on peut observer (cliquez sur celles-ci pour avoir un agrandissement) :

Il faudra sans doute aider les élèves à se poser des questions, les consignes étant très vagues. Nous pouvons en tous cas les guider afin qu’ils comprennent les points suivants :

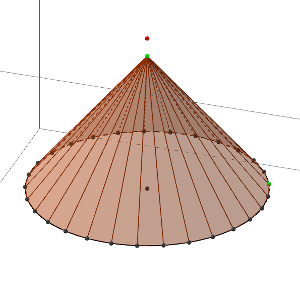
• le lien entre la pyramide et le cône lorsque l’on accroît le nombre de côtés du polygone de base (point orange)
• la nature de la section d’une pyramide et d’un cône, une description de la manière de couper la pyramide (point rouge).
• une description du patron d’une pyramide en fonction du nombre de côtés du polygone et en fonction de la position du sommet par rapport à la base.

Pour inciter les élèves à la manipulation, nous pouvons leur demander de déterminer le nombre de sommets, de faces et d’arêtes en fonction du nombre de côtés de la base (des exemples d’abord puis une généralisation).

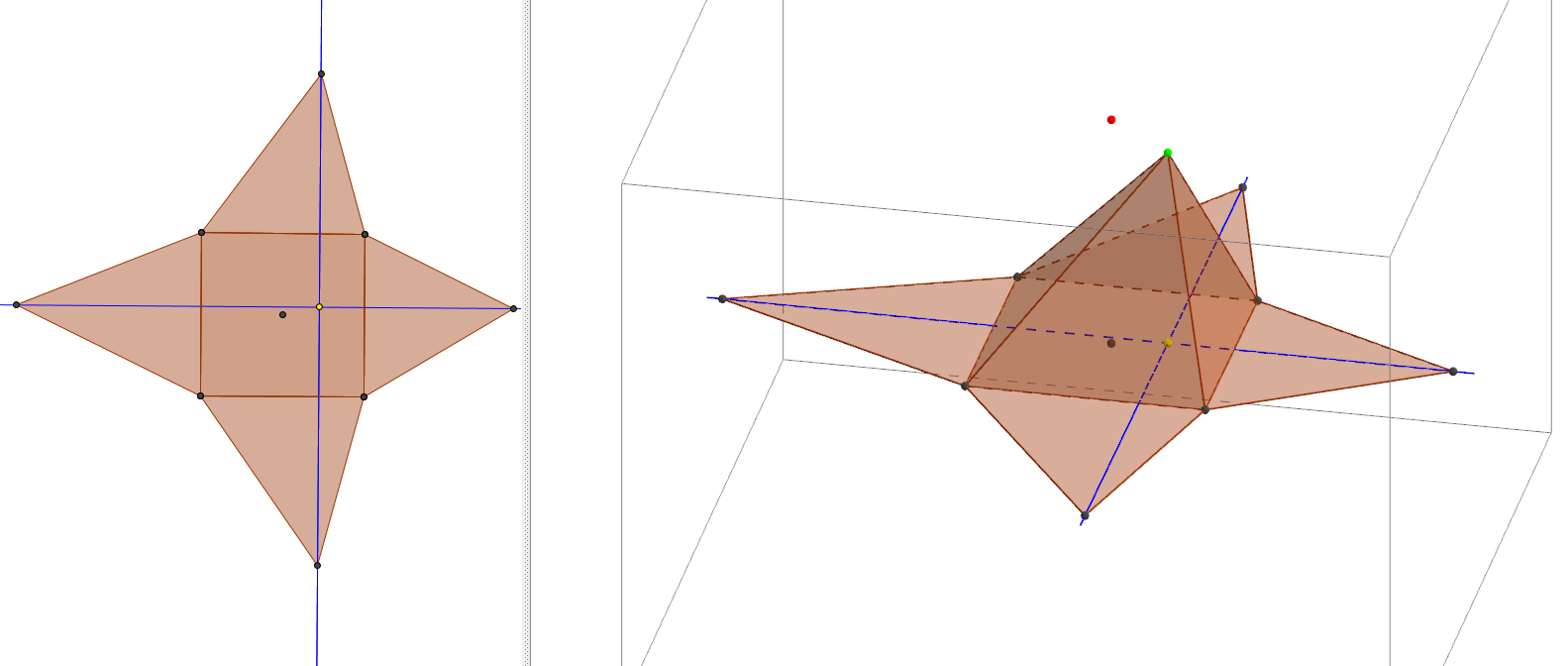
Pour le travail sur les patrons, nous pouvons demander aux élèves de positionner le sommet d’une pyramide à base carrée dans différentes positions (au dessus d’un des sommets de la base, au dessus du milieu d’une arête de la base, la projection se trouvant à l’intérieur de la base, à l’extérieur...) et d’observer l’effet sur le patron. Nous pouvons ensuite leur demander de conjecturer à propos de la position du projeté orthogonal du sommet sur le patron en se plaçant dans la fenêtre 2D. Le propos est illustré ci-dessous.
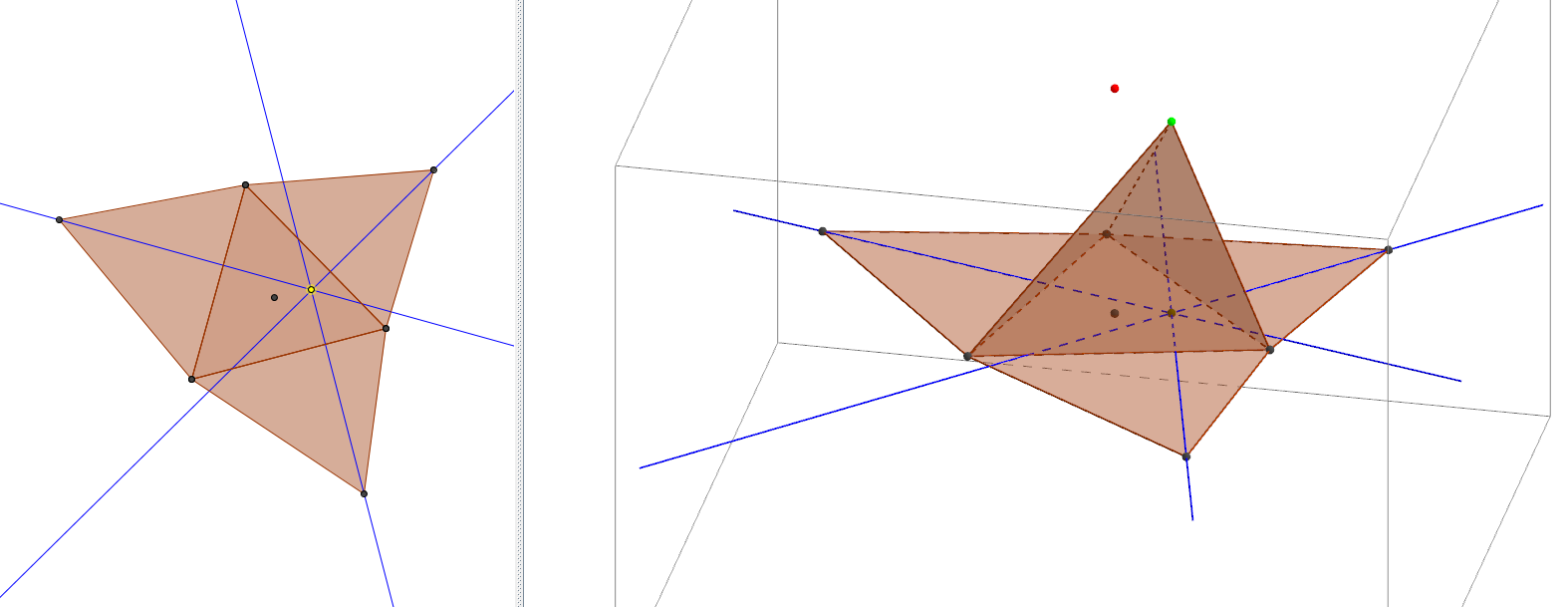
Un travail similaire peut être demandé sur le projeté orthogonal en prenant comme base un polygone ayant un nombre impair de côté (triangle, pentagone par exemple).

Attention : il faut utiliser l’outil "droite" pour joindre les sommets du patron dans la fenêtre 2D, le tracé d’un segment sur le patron peut faire planter Géogebra.