Accompagnements La troisième dimension
(Le livre en version numérique)

---

Accompagnements

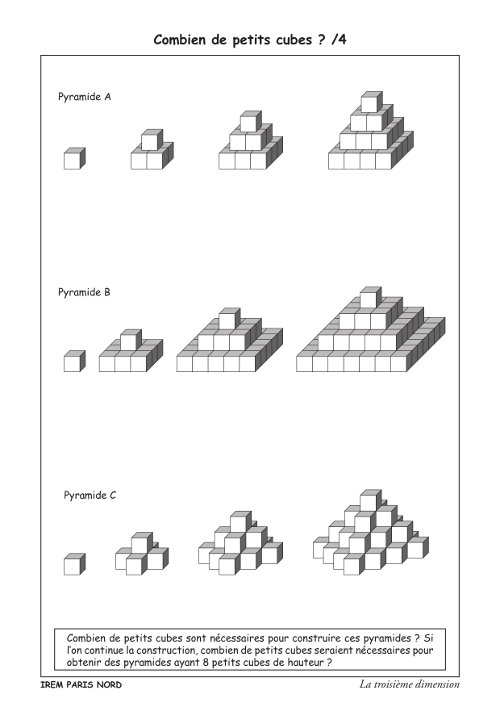
Pyramide A

1) Les premières étapes

Pour les premières étapes, l’observation peut-être suffisante.
étape 1 : 1 cube
étape 2 : 1 + 4 = 5 cubes
étape 3 : 5 + 9 =14 cubes
étape 4 : 14 + 16 = 30 cubes

2) Les étapes suivantes

Ensuite, il faut avoir saisi la logique de passage d’une étape à l’étape suivante en faisant apparaître les carrés.
étape 5 : 30 + 5² = 55 cubes
étape 6 : 55 + 6² = 91 cubes
étape 7 : 91 + 7² = 140 cubes
étape 8 : 140 + 8² = 204 cubes

3) Pour aller plus loin

Nous pouvons reprendre la même question en augmentant la hauteur des pyramides (par exemple 20 puis 50 cubes de hauteur).
Cela place les élèves devant les limites de la méthode précédente.

Nous pouvons alors leur proposer un travail de réflexion sur l’écriture numérique de chaque étape qui aboutirait à ceci :

étape 1 : 1
étape 2 : 1+2²
étape 3 : 1+2²+3²
.........................................................
étape 8 : 1+2²+3²+4²+5²+6²+7²+8²
.........................................................
étape 20 : 1+2²+3²+ ... + 19²+20²

L’étape 20 est encore réalisable à la calculatrice mais beaucoup d’erreurs risquent de survenir. Quant à l’étape 50, le découragement risque d’être le principal obstacle à la résolution du problème.

Nous pouvons alors leur proposer la formule de la somme des carrés des n premiers entier :

Un travail sur le sens de cette formule et sur son utilisation dans le cadre de notre problème permettra de travailler le sens de la lettre dans une expression.

Pour pimenter la recherche, nous pouvons leur proposer le problème suivant :
"Quelle est la hauteur d’une pyramide constituée de 318 549 cubes ?".
Beaucoup d’essais seront nécessaires pour répondre à cette question.

4) Quelques précautions sur l’utilsation pédagogique des formules

L’introduction de la formule précédente nécessite quelques précautions. Il nous semble pertinant de la proposer à partir de la classe de 4è. De plus, il est impératif de dire aux élèves qu’une démarche mathématique permet de l’obtenir et qu’ils n’en maîtrisent pas les outils. Cela afin qu’ils ne la considère pas comme "tombée du ciel".
Nous pourrons éventuellement leur montrer ou leur faire découvrir par eux-même un problème similaire qui se trouve à leur portée comme la somme des n premiers nombres entiers. Un article détaillé sur la méthode découverte par Carl Friedrich Gauss se touve sur cette page.

Pyramide B

Le principe est identique à la pyramide précédente. Cette fois, il s’agit de la somme des carrés des n premiers nombres entiers impairs.

Cette somme se calcule à l’aide de l’expression suivante :

La difficulté supplémentaire par rapport à la pyramide précédente se trouve dans la différence entre le nombre d’étapes (n) et le nombre que l’on ajoute à l’étape suivante (2n-1)².

Pyramide C

Une généralisation pour cette pyramide n’est pas souhaitable car trop difficile. Nous nous contenterons donc de l’énoncé tel qu’il est posé et nous le réserverons aux élèves les plus avancés.
Cela demande déjà beaucoup d’organisation.
Voici une proposition de solution (d’autres raisonnements sont possibles) :

étape 1 : 1 cube
étape 2 : 1 + 5 = 6 cubes
étape 3 : 6 + (5 + 2 x 4) = 6 + 13 = 19 cubes
étape 4 : 19 + (13 + 3 x 4) = 19 + 25 = 44 cubes
étape 5 : 44 + (25 + 4 x 4) = 44 + 41 = 85 cubes
étape 6 : 85 + (41 + 5 x 4) = 85 + 61 = 146 cubes
étape 7 : 146 + (61 + 6 x 4) = 146 + 85 = 231 cubes
étape 8 : 231 + (85 + 7 x 4) = 231 + 113 = 344 cubes

Il y a donc 344 cubes qui composent la pyramide C à la 8è étape.