
Sections de cubes et de pyramides
1. Introduction : Pourquoi commencer par l’étude des sections ?
Le travail sur la perspective et les sections est primordial avant de s’intéresser aux patrons. Ainsi, même si nous ne sommes pas sensés traiter des sections en classe de 4è, il nous apparaît nécessaire de le faire avant d’aborder l’étude des pyramides.
Le travail sur les sections d’un cube doit permettre à l’élève de "manipuler" la perspective cavalière et de faire le lien entre l’espace (le solide) et le plan (la section).
De plus, en étant confronté à des problèmes qui nécessiteront des justifications au sein de la classe, chaque élève devra appuyer son point de vue par des raisonnements assez naturels qui font appel aux figures semblables (par exemple, justifier l’égalité de deux longueurs comme étant deux diagonales de carrés de même dimension...).
Enfin, en classe de 4è, l’élève sera confronté à des problèmes de calcul de longueur dans l’espace. Cela représente souvent des difficultés importantes car il faut à la fois disposer d’une vision dans l’espace claire et maîtriser les théorèmes de géométrie plane, en particulier le théorème de Pythagore.
Bien souvent, la résolution de ces problèmes revient à chercher un triangle rectangle dans lequel se trouve la longueur que l’on doit calculer. Beaucoup d’élèves ne voient pas ce triangle même après correction. Cela provient sans doute du fait que ce triangle n’a pas d’existence matérielle pour l’élève.
Par contre, la section d’un solide a une existence plus palpable. Ainsi, si l’élève a pris l’habitude de considérer la longueur à calculer comme étant une longueur à l’intérieur d’une section, ces problèmes présenteront des difficultés moindres.
Par exemple : le calcul de la longueur de la diagonale d’un cube

Calcul de la diagonale comme étant l’hypoténuse d’un triangle rectangle
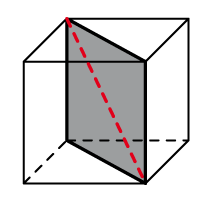
calcul de la diagonale comme étant la diagonale du rectangle qui sectionne le cube en deux morceaux identiques
2. Activités papiers : aborder les sections d’un cube
C’est l’occasion de constater que la perspective cavalière déforme, que deux figures planes de même dimensions peuvent être représentées différemment. Cela aboutit très vite à la nécessité de mettre en place des petits raisonnements afin de convaincre, en lieu et place des "Ça se voit" parce que justement ce n’est pas le cas. Ces raisonnements portent surtout sur la disposition des sommets de la section.
- utiliser le compas pour reporter des longueurs d’une figure à l’autre. Un travail doit être effectué pour savoir quelles longueurs sont représentées en vraie grandeur dans un figure dessinée en perspective cavalière.
- affiner les raisonnements qui devront porter cette fois sur les longueurs de figures semblables.
Le cas du losange mérite que l’on s’y arrête. En effet, il n’est pas si facile de convaincre de sa nature et surtout d’affirmer que ce n’est pas un carré... Pensez aux diagonales !!
La 2è partie de la question, qui consiste à écrire les dimensions de la section en fonction de a, est à aborder une fois que le théorème de Pythagore a été étudié et comme exercice de synthèse donc ultérieurement.
2. Activités papier : Tracé de sections de cubes et de pyramides








