I. Présentation

Geogebra depuis sa version 5 intègre une fenêtre 3D dans laquelle nous pouvons évoluer dans l’espace. Cette intégration est récente, donc imparfaite mais permet tout de même de travailler avec les élèves. Les fonctionnalités s’amélioreront au fil du temps à n’en pas douter.

Nous ne présentons ici que des exemples d’utilisation possible par les élèves que ce soit en classe (avec un vidéo-projecteur) ou en salle informatique, l’objectif étant de leur faire manipuler des solides, des sections, des patrons ...
Bien que les fichiers proposés puissent servir de démonstration devant les élèves, ce n’est pas leur finalité. Il existe sur le net foison de fichiers Geogebra de meilleure qualité et plus adaptés à la seule visualisation. Il est possible aussi de les créer soi-même.

Toutes les activités Géogebra3D disponibles sur ce site sont regroupées dans la section "Les accompagnements du livre La troisième dimension" (suivre ce lien).

II. L’interface

L’interface 3D est assez complète et complexe pour des élèves de collège : on y trouve beaucoup d’outils présents dans la fenêtre classique de géométrie plane et d’autres spécifiques à la géométrie dans l’espace. Ainsi, pour que les élèves puissent l’utiliser sans trop de difficultés, il est nécessaire de limiter les outils mis à leur disposition (voir "barre d’outils personnalisée" du menu "outils").

Il peut être utile dans certain cas de garder ouverte la fenêtre 2D. En effet, elle correspond au plan (xOy) de la fenêtre 3d. Ces deux fenêtres sont liées c’est à dire que tout ce qui est construit dans l’une apparaît dans l’autre. Cela permet aux élèves de mieux appréhender la géométrie dans l’espace.

III. Quelques exemples

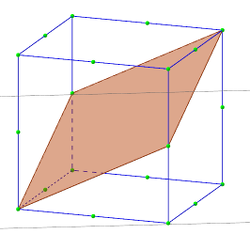
1. Construire des sections

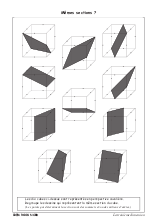
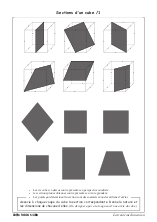
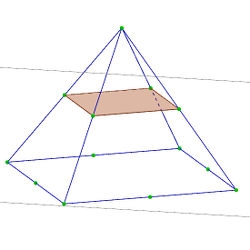
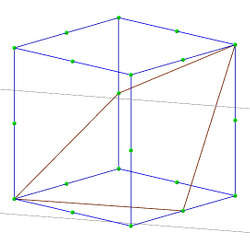
Nous proposons une ou plusieurs des activités suivantes tirées du livre La troisième dimension dont l’objectif est d’aborder les sections du cube et de la pyramide.

Ces activités ont été construites pour se suffire à elle-mêmes mais nous pouvons utiliser les deux fichiers GeoGebra suivants afin de faire construire par les élèves les sections proposées, collectivement en classe entière ou individuellement en salle informatique (cliquez sur les images pour obtenir le fichier).

La manipulation de l’espace graphique 3D permet aux élèves de mieux visualiser, de comprendre facilement la notion de vue. De plus, il peuvent vérifier rapidement si leur section est bien plane. En effet, l’outil "polygone" ne fait apparaître de surface que si le polygone se situe dans un plan, sinon il reste vide (voir le fichier suivant).

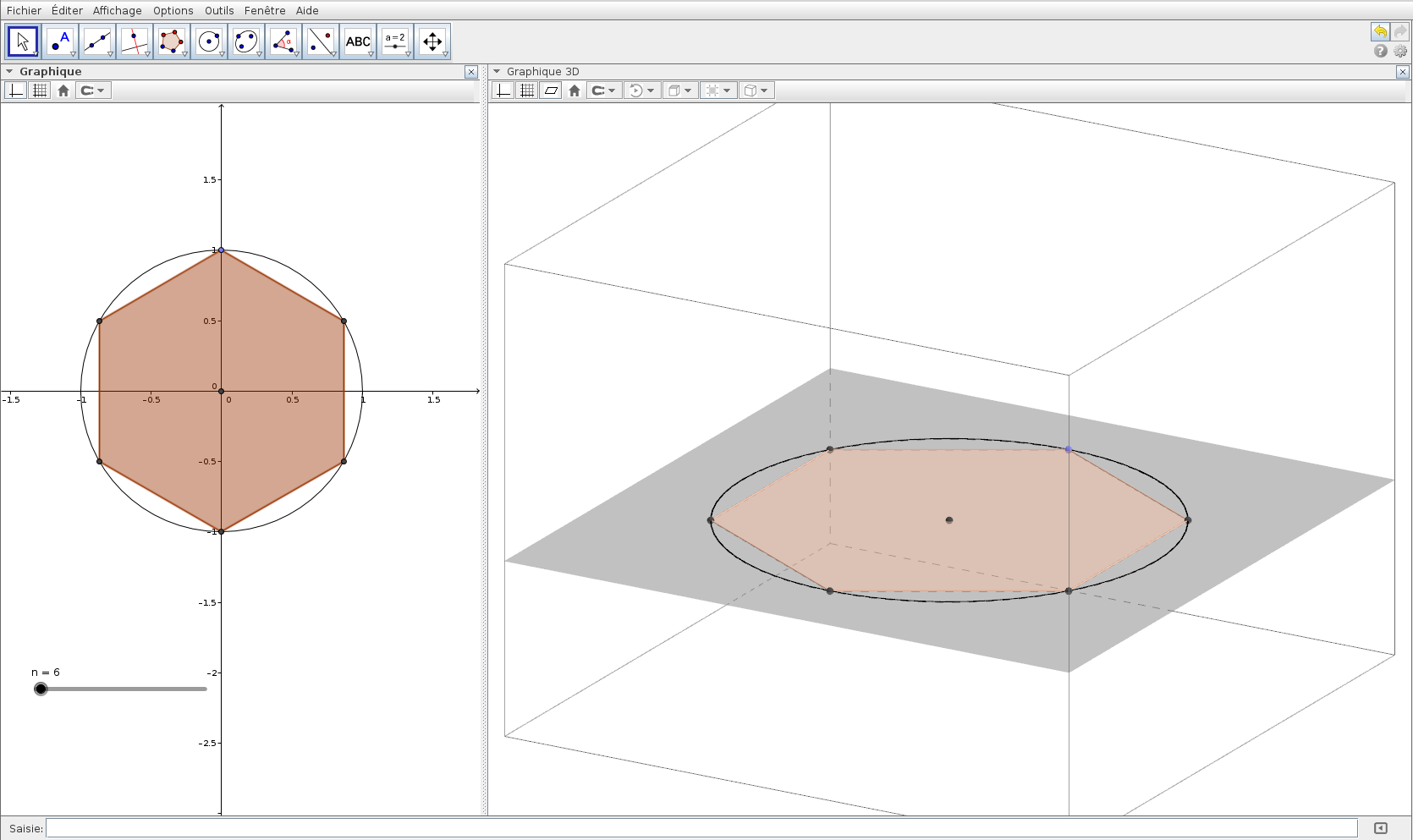
2. Visualiser-manipuler un solide

Dans l’activité suivante, le support est uniquement informatique sous la forme d’un fichier Geogebra. Les élèves devront produire un compte-rendu de ce qu’ils ont observé, manipulé et constaté.

Les consignes suivent trois phases :

• Observer/décrire les pyramides en manipulant les points colorés verts et oranges.
• Utiliser l’outil "lier/libérer un point" pour pouvoir déplacer le sommet de la pyramide dans n’importe quel sens. Déplacer les points et observer/décrire.
• Utiliser l’outil "patron", un nouveau curseur apparaît. Déplacer les points puis observer/décrire.
• Observer/décrire la section d’une pyramide en déplaçant le point rouge.

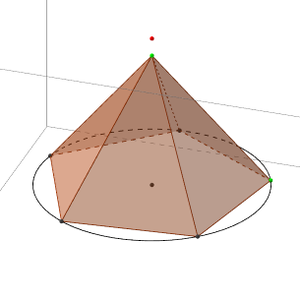
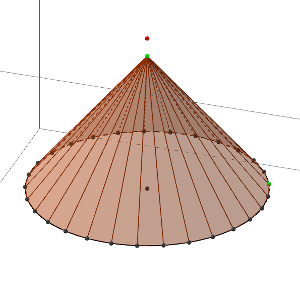
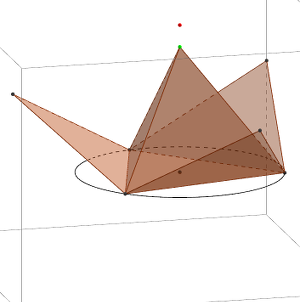
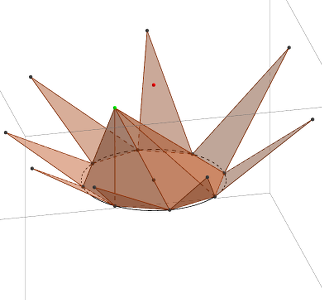
Voici quelques captures d’écran de ce que l’on peut observer (cliquez sur celles-ci pour avoir un agrandissement) :

Il faudra sans doute aider les élèves à se poser des questions, les consignes étant très vagues. Nous pouvons en tous cas les guider afin qu’ils comprennent les points suivants :

• le lien entre la pyramide et le cône lorsque l’on accroît le nombre de côtés du polygone de base (point orange)
• la nature de la section d’une pyramide et d’un cône, une description de la manière de couper la pyramide (point rouge).
• une description du patron d’une pyramide en fonction du nombre de côtés du polygone et en fonction de la position du sommet par rapport à la base.

Pour inciter les élèves à la manipulation, nous pouvons leur demander de déterminer le nombre de sommets, de faces et d’arêtes en fonction du nombre de côtés de la base (des exemples d’abord puis une généralisation).

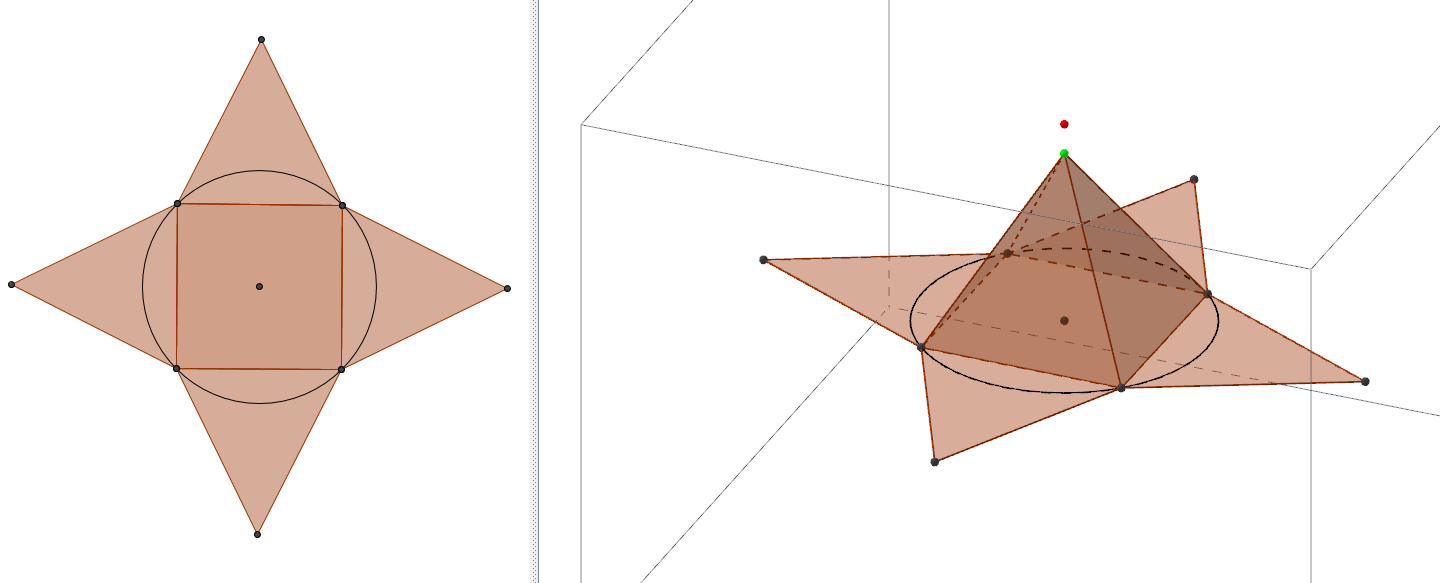
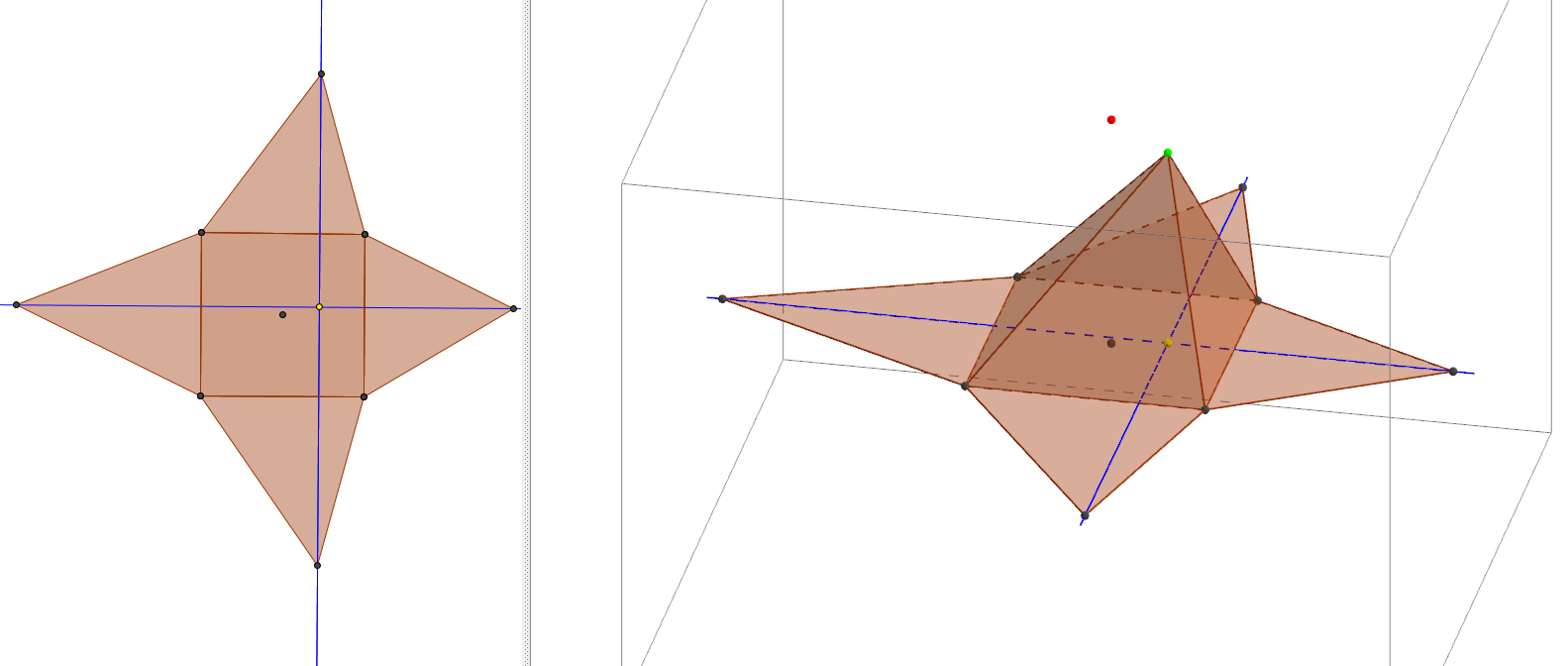
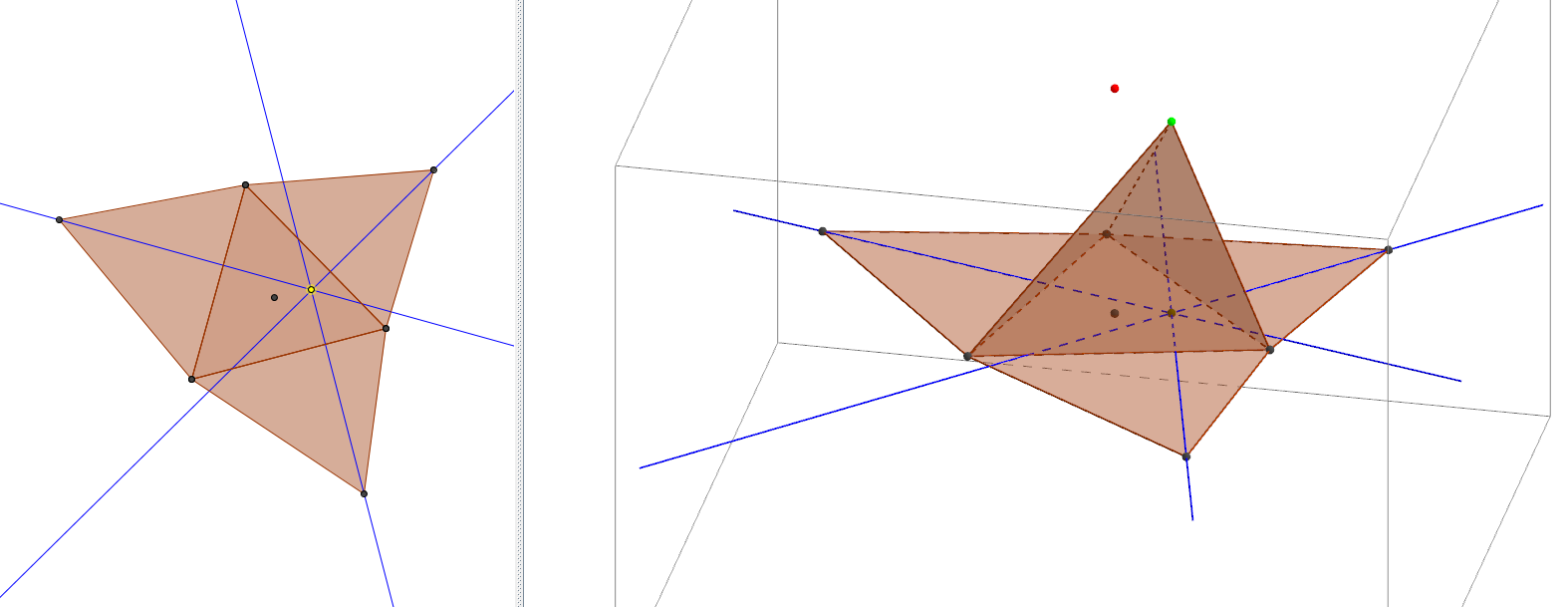
Pour le travail sur les patrons, nous pouvons demander aux élèves de positionner le sommet d’une pyramide à base carrée dans différentes positions (au dessus d’un des sommets de la base, au dessus du milieu d’une arête de la base, la projection se trouvant à l’intérieur de la base, à l’extérieur...) et d’observer l’effet sur le patron. Nous pouvons ensuite leur demander de conjecturer à propos de la position du projeté orthogonal du sommet sur le patron en se plaçant dans la fenêtre 2D. Le propos est illustré ci-dessous.
Un travail similaire peut être demandé sur le projeté orthogonal en prenant comme base un polygone ayant un nombre impair de côté (triangle, pentagone par exemple).

Attention : il faut utiliser l’outil "droite" pour joindre les sommets du patron dans la fenêtre 2D, le tracé d’un segment sur le patron peut faire planter Géogebra.

Cette activité peut être déclinée avec les autres solides étudiés au collège : prisme, cylindre, cône. Des fichiers Geogebra sont disponibles dans la section "Les accompagnements du livre La troisième dimension", suivre ce lien.

Ces exemples ne sont que des illustrations de ce qu’il est possible de faire avec les élèves en utilisant la fenêtre 3D de Geogebra, le point essentiel étant de simplifier au maximum les outils et la situation.