Le chasse-nombre est un matériel pédagogique à réaliser soi-même. Il est à destination des élèves de cycle 2.
L’article de Présentation de Rubricamaths a été complété. Celui-ci détaille les principales démarches qu’il est possible de mettre en oeuvre avec les activités informatiques présentes.
La gazette n°1 est sortie.
Vous y trouverez les dates et les modalités d’inscription et de passation.
La gazette n°1 est sortie.
Vous y trouverez les dates, les modalités d’inscription et de passation.
“Mise” à jour de la série "Visualiser pour calculer et utiliser des variables" afin d’améliorer la visibilité des solides.
Mise à jour de la série "Visualiser pour calculer (1)" afin d’améliorer la visibilité des solides.
Remarque importante sur les fichiers :
Les fichiers marchent très bien en local, c’est-à-dire lorque les fichiers sont téléchargés puis ouverts avec une version récente de Geogebra installé sur l’ordinateur. Par contre, ces fichiers ouverts directement depuis le navigateur (en ligne) peuvent parfois avoir quelques bugs et être assez lent.
Sommaire
- Présentation des fichiers
- Démarches et utilisations
- Progression et résultats attendus
- Pour continuer
Présentation des fichiers
Il faut déterminer l’expression du périmètre et de l’aire de la figure (ou la longueur de la ligne brisée) en fonction de n. Cette expression devra être saisie dans la dernière ligne du tableur. L’élève pourra compléter les lignes précédentes du tableur pour faire des essais et des conjectures. Toutes les réponses, numériques ou littérales, sont validées (vert) ou invalidées (rouge).
Toutes les expressions numériques ou littérales équivalentes sont acceptées et validées. Ainsi :
- la saisie de 24 sera acceptée au même titre que la saisie de 4 x 6 ou 2 x (7 + 5).
- la saisie de 4 x (n+1)² sera acceptée au même titre que la saisie de 4n² + 8n + 4
Cela permet de valider les expressions quelque soit le raisonnement utilisé par l’élève.
Les objectifs de cette séquence sont multiples :
- Travailler la production d’expressions littérales :
- analyser une situation géométrique,
- chercher les invariants et la variable de cette situation,
- conjecturer à l’aide de nombre une expression littérale.
- Gérer l’hétérogénéité en proposant des activités de recherche à la fin de la série.
Les expressions en fonction de n attendues sont :
– Périmètre = 4n + 8
– Aire = (n + 2)² - 4 ou n² + 4n
Démarches et utilisations
Produire une expression littérale est l’une des compétences les plus difficile et les plus importante que l’élève doit travailler au collège. Lorsque l’on propose des situations dans lesquels une variable intervient, il n’est pas rare d’être confronté à l’incompréhension de l’objectif final par beaucoup d’entre eux et par conséquent à une grande passivité d’une partie de la classe.
Le premier objectif de cette série d’activités est justement d’essayer de rendre actif l’élève en lui permettant de manipuler lui-même les figures (à l’aide du curseur) et de rentrer progressivement dans le problème en complétant l’aire et le périmètre dans le tableur à l’aide de valeurs numériques. Il est de plus rassuré dans sa progression par des validations à chaque saisie quelque soit le raisonnement qu’il utilise.
Un élève ayant compris le principe sur les premières étapes numériques peut alors essayer de rentrer une formule de tableur dans les cellules suivantes, par exemple : A7 x A7 + 4 x A7
Il pourra ainsi vérifier si sa formule est correcte notamment lorsque n est égal à 100 et lorsque n est égal à un nombre aléatoire.
Ensuite, il pourra proposer une formule écrite à l’aide de la variable n dans la dernière cellule du tableur. L’objectif final étant de produire une formule, les étapes précédentes ne sont pas nécessaires. Un élève ayant compris rapidement peut tout à fait saisir directement l’expression en fonction de n.
Voici une vidéo illustrant l’ensemble des propos tenus ci-contre (cliquez sur l’image pour la lancer) :
Pour résoudre le problème précédent, plusieurs démarches sont possibles :
l’expression peut s’écrire : (n+2)² - 4
l’expression peut s’écrire : n² + 4n
l’expression peut s’écrire : n(n+2) + 2n
Comment accompagner les élèves ?
Plusieurs points de blocage peuvent se rencontrer durant le travail sur cette série d’activités.
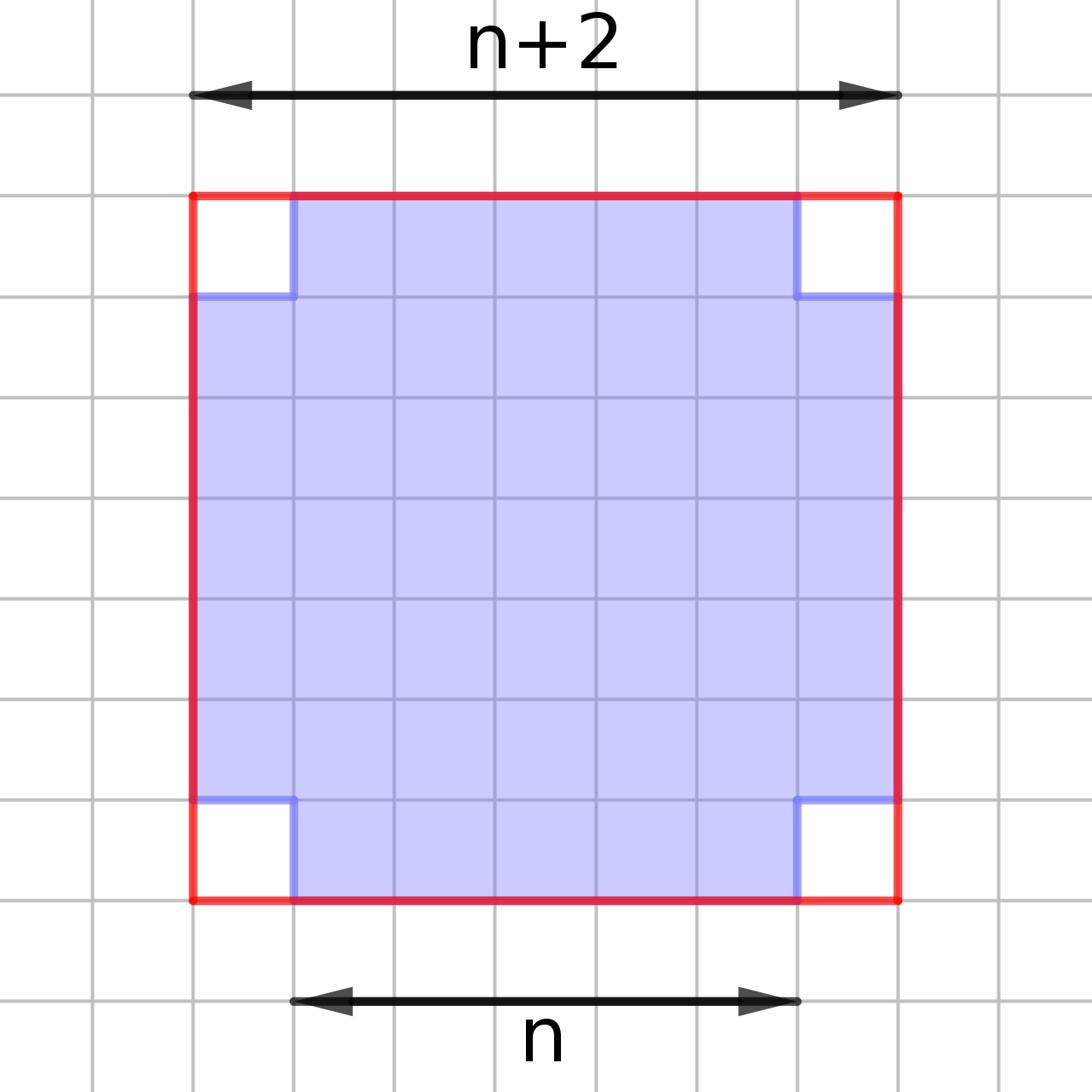
1) Pour certains élèves, le saut entre les premiers résultats numériques et la production de l’expression (ou de la formule tableur) est trop important. D’ailleurs, la plupart trouvent rapidement une relation de récurrence sur les premières étapes numériques mais se trouvent quelque peu désemparés lorsqu’il s’agit de trouver le résultat pour n=100. Pour les amener progressivement vers l’expression littérale et pour les inciter à délaisser les relations de récurrence, on peut leur conseiller d’écrire la suite de calcul sur une seule ligne conduisant au résultat (par exemple à partir de n=3). En reprenant l’exemple du carré tronqué (1), cela donne ce genre d’expression :
- pour n=3, aire = 3 x 3 + 4 x 3
- pour n=4, aire = 4 x 4 + 4 x 4
- pour n=5, aire = 5 x 5 + 4 x 5
- ...
2) Certains élèves oublient la situation géométrique pour ne se concentrer que sur les suites de nombres. Pourtant, l’étude de cette situation géométrique peut leur permettre d’être plus efficace. Il est donc nécessaire de rappeler les questionnements qu’ils doivent avoir face à de tels problèmes (lors de bilans collectifs et lors d’intervention individuelle auprès des élèves) :
- qu’est-ce qui bouge dans la figure ?
- qu’est-ce qui reste fixe ?
- A quoi correspond la variable n dans la figure ?
- De quelles figures est composée la figure étudiée ?
L’utilisation d’un brouillon sur lequel ils peuvent faire des schémas, annoter, faire des calculs intermédiaires peut s’avérer très utile et débloquer bien des situations.
Utilisations
Cette série d’activités peut être utilisée collectivement en classe (dans ce cas, c’est l’enseignant qui réalise les manipulation) ou bien de manière individuelle sur un support numérique (tablette, PC en salle informatique ...) que ce soit en classe ou à la maison. Ces deux manières d’utiliser les activités peuvent évidemment être menées conjointement.
Progression et résultats attendus
La progression proposée sur Rubricamaths est basée sur une complexification progressive des situations.
Quelques figures très difficiles sont proposées à la fin de la série pour occuper les élèves en avance.
Ci-dessous, les réponses attendues pour chacune des activités :
• Aire = n²
• Aire = 6n
• Aire = 4 x (2n + 1) ou 8n + 4
• Aire = 4n + 1
• Aire = (n+2)² - 4
• Aire = 5n²
• Aire = n(n+1)
• Aire = 2n²
• Aire = (n-1)² + 2n
• Aire = 2n² - 1
• Aire = (2n + 1)² - 4
• Aire = (2n)² + 4 ou 4n² + 4
• Aire = n² + 2n +2
• Aire = (2n + 1)² - n²
• Aire = 5n² - 4
• Aire = (2n + 1)² - 4
• Aire = 12n² - 8n + 1
Pour continuer
Cette série d’activités prend place parmi d’autres séries d’activités informatiques consacrées à des degrés divers à la variables.
- Comme il a été évoqué précédemment, un travail sur la production d’expressions numérique sur une seule ligne est une étape importante dans la production d’expressions littérales. La série d’activités suivante est consacrée à ce thème : Compter des cubes.
- Un travail plus spécifique sur les fonctions : boîtes noires.
- Deux séries reprenant le même principe mais cette fois dans l’espace :
- une plus simple : Solides et variables discrètes.
- une de difficulté équivalente : Structure de cubes et variables discrètes.
- Pour ne pas se cantonner aux variables discrètes, un travail sur les variables continues nous semble nécessaire : Figures et variables continues
- Quelques problèmes d’optimisation mettant en œuvre les propriétés de collège (théorème de Pythagore et Thalès, trigonométrie) ainsi que les fonctions et leur représentations graphiques : situation problèmes et fonctions
Nous rappelons, pour finir, que tout travail réalisé sur des fichiers informatiques doit être accompagnés de bilans collectifs et mené conjointement à un travail sur support papier sous la supervision d’un enseignant.
