Le projet a été réalisé durant l’année 2016-2017 dans la classe de 5è03 du Collège Condorcet (Paris) et imaginé par Jean-Baptiste Olin (français) et Stéphan Petitjean (maths).

Il a été reconduit durant l’année 2017-2018 dans la classe de 5è01 du même établissement scolaire. Le projet a été quelque peu modifié, tant en Français qu’en mathématiques, afin de le rendre plus efficace auprès des élèves.
Ces améliorations sont décrites en fin d’article, le reste étant la description du projet initial.

Sommaire du projet originel (2016-2017)

• Description du projet pluridisciplinaire

• Le travail en mathématique : Les arts de l’Islam
  • La visite au musée
  • Du pavage au motif minimal
  • Du motif minimal au pavage

• Les productions liées au projet

• Retour d’expérimentation et évolutions possibles

• Quelques liens et livres

Sommaire du projet 2017-2018

• Quelques modifications et améliorations par rapport au projet originel

• Observation et création de pavage islamique

• Quelques travaux d’élèves

• Les productions liées au projet 2017-2018

• Retour d’expérimentation

Article écrit par Stéphan Petitjean (contact)

Description du projet pluridisciplinaire

Le projet est construit autour de quatre visites au musée du Louvre. Chaque visite a une thématique différente. Les disciplines se regroupent autour de ces thématiques à des degrés différents.

• 1ère visite : Découverte du musée du Louvre (Histoire, Français)
• 2ème visite : Les arts de l’Islam (Maths, Français, Histoire)
• 3ème visite : La mythologie antique (Latin, Français, Histoire, Maths)
• 4ème visite : La renaissance (Arts plastiques, Maths, Histoire)

Le travail autour des arts de l’Islam s’articule autour de deux disciplines principalement, le Français et les Mathématiques, de la manière suivante :

• en Français :
  • La découverte d’œuvres et d’objets ayant une portée culturelle et architecturale lors de la visite au musée.
  • un travail de lecture et d’écriture autour de Sindbad le marin.

• en Mathématiques :
  • La découverte d’œuvres et d’objets comportant des pavages décoratifs lors de la visite au musée.
  • un travail sur papier dont l’objectif est d’extraire le motif minimal permettant le pavage.
  • un travail utilisant l’outil informatique dont l’objectif est de construire le pavage à partir du motif minimal.

La suite de cet article présente le travail effectué en mathématique, le travail en français sera évoqué dans la partie consacrée aux productions liées au projet.

Le travail en mathématique : La visite au musée

La visite est organisée sous la forme d’un rallye. Les élèves sont regroupés par 3 ou 4 et doivent trouver les œuvres à partir d’énigmes. Toutes les œuvres se situent dans la grande salle du bas du pavillon des arts de l’Islam du musée du Louvre. Une fois découvertes, ils doivent les photographier, localiser leur provenance sur un fond de carte puis venir voir un adulte pour confirmation.

Trois énigmes sont données au départ à chaque groupe. Des indices supplémentaires sont prévus dans le cas où un groupe serait bloqué. Lorsqu’un groupe a trouvé les solutions des trois énigmes, d’autres lui sont proposées.

Ce rallye dure environ 45 minutes.

Les œuvres à découvrir sont les suivantes :

Le travail en mathématique : Du pavage au motif minimal

Le travail proposé aux élèves se réalise en classe à partir d’activités sur support papier. Les élèves sont en groupe (les mêmes que pour la visite).
L’objectif du travail est d’isoler le motif minimal de chacun des pavages provenant des objets repérés lors de la visite.
Chaque groupe doit étudier au moins trois pavages.

Le travail sur ces activités dure environ 1h 30 min.

Les fiches de travail sont les suivantes :

Quelques activités complémentaires (pour les groupes en avance) :

Le travail en mathématique : Du motif minimal au pavage

Le travail proposé se réalise en salle informatique en utilisant le logiciel Geogebra. Les élèves travaillent individuellement.
L’objectif, cette fois, est de réaliser le pavage à partir du motif minimal, c’est-à-dire de faire la démarche inverse du travail proposé précédemment.

Chacun des fichiers est configuré de la même manière et comporte :

• une image permettant d’identifier le pavage.
• une barre d’outil simplifiée facilitant l’accès aux transformations.
• le motif minimal du pavage.

Pour réaliser le pavage, il est nécessaire de tracer l’élément caractéristique de la transformation (droite, point, vecteur) puis d’appliquer la transformation correspondante (symétrie axiale, symétrie centrale ou rotation, translation).
Il est possible de sélectionner plusieurs éléments à transformer (en utilisant un clic droit) avant d’effectuer la transformation.
Plusieurs méthodes de construction sont possibles, les élèves sont donc laissés libres. Le professeur pourra montrer au besoin des manières de procéder plus efficaces, comme l’utilisation de la translation.
Lorsque la méthode de pavage semble maîtrisée par un élève, on lui laisse la possibilité de créer sa propre figure. Celles-ci seront sauvegardées et utilisées pour la production finale du projet.

La durée de ce travail sur support informatique est de 2h.

Les fichiers de travail sont les suivants (cliquez sur l’image pour ouvrir les fichiers Geogebra dans le navigateur) :

Les productions liées au projet

Vous trouverez ci-dessous le livret regroupant l’ensemble des productions des élèves :

• Les textes réalisés en Français autour de Sindbad le marin.
• Les figures réalisées à l’aide de Geogebra autour des pavages.

Quelques précisions concernant le travail en français

Dans le cadre de l’objet d’étude portant sur le voyage et l’aventure, les élèves ont étudié les Voyages de Sindbâd pour leur faire saisir la similitude de démarche entre les artisans et les conteurs du Moyen-Orient. Dans les arts de L’Islam, le foisonnement décoratif nait de la duplication d’un même motif démultiplié en jouant des ressources des différentes symétries. De même les sept voyages de Sindbâd sont construits à partir d’un nombre limité de motifs narratifs que les conteurs reprennent et transforment de récits en récits : tempête, attaque d’un monstre, rivière souterraine, île paradisiaque, naufrage...
Les élèves ont appris dans un premier temps à identifier ces motifs narratifs et à repérer la structure commune à tous les voyages de Sindbad. Tout au long de la séquence, le travail sur les textes était réinvesti dans la production d’écrits intermédiaires : description d’une île idéale, invention d’une créature terrifiante, récit d’un naufrage.... En fin de séquence, tout ce travail a abouti à la rédaction par groupes de deux ou trois élèves du huitième voyage de Sindbâd. Chaque récit devait par ailleurs intégrer une œuvre choisie dans les collections des arts de l’islam. Ces écrits sont rassemblés dans un recueil illustré par les travaux de mathématiques .

Dans le cadre de l’histoire des arts, une dizaine d’objets ont été présentés sur place aux élèves afin de leur faire découvrir la variété des collections des arts de l’islam et de les faire réfléchir aux échanges avec la culture occidentale, échanges particulièrement sensibles dans l’histoire de certains objets comme le baptistère de Saint-Louis ou le globe céleste d’Asturlabi.

Jean-Baptiste Olin

Retour d’expérimentation et évolutions possibles

Retour d’expérimentation

La visite et le travail informatique n’ont posé aucun problème.

Le travail sur papier, par contre, a demandé un temps d’adaptation important. Durant la première séance de 45 minutes, plusieurs groupes n’ont pas saisi l’objectif final et ont piétiné. Les consignes données dans les fiches d’activités n’ont pas suffi ou n’étaient pas assez explicites. Les groupes ayant commencé par les pavages à base de ligne ont davantage été mis en difficulté que ceux ayant commencé par les pavages à base d’image. Une reprise a donc été nécessaire en classe entière. Elle a pris l’aspect d’une présentation imagée d’une démarche permettant d’isoler le motif minimal d’un pavage (pour obtenir le document, suivre ce lien). La deuxième séance de travail en groupe a été beaucoup plus efficace à la suite de cette reprise.

Évolutions possibles

Premier point
Personnellement, je regrette de n’avoir pu intégrer davantage d’œuvres provenant d’Espagne et du Maghreb. La collection du Louvre, bien qu’importante, ne dispose pas d’objets avec des pavages utilisables en classe provenant de ces régions du monde. Il pourrait être pertinent de faire quelques entorses au projet en proposant quelques œuvres qui ne font pas partie de la collection du Louvre. Ces œuvres pourrait avoir été rencontrées par les élèves en histoire (décors de Mosquée, de medersa, de palais ...) puis étudiées en mathématique. Cela permettrait, en outre, davantage de liberté dans le choix des œuvres, de leur provenance et dans le choix des types de pavages, s’appuyer sur une collection de musée étant très contraignante.

Deuxième point
Plusieurs élèves ont regretté de ne pouvoir colorier à leur convenance leurs figures réalisée sur Geogebra, principalement celles composées de lignes. En effet, le logiciel ne le permet pas facilement surtout que le nombre d’objets est très important. Pour palier à cet inconvénient, il est possible d’envisager, pour les pavages à base de lignes, d’utiliser le logiciel GéoTortue car il permet de colorier de manière intuitive et aisée les figures réalisées. De plus, la manière de réaliser le pavage avec une tortue est complètement différente de celle employée avec Geogebra. Cela peut permettre aux élèves de mettre en œuvre différemment leurs connaissances des transformations. Il faudra bien sûr que les élèves soient formés antérieurement à l’utilisation de ce logiciel de programmation.

Voici quelques fichiers .xrt relatif aux œuvres qui ont été donnés à certains élèves de la classe plus tard dans l’année, le projet étant alors clos et la production finale déjà achevée (cliquez sur les images pour obtenir le fichier) :

Les fichiers .xrt sont à ouvrir directement à partir du logiciel GéoTortue.

Pour avoir une idée de la réalisation d’un pavage avec une tortue, en l’occurrence, l’œuvre 3, vous pouvez cliquez sur l’image ci-dessous. L’animation est réalisée avec le logiciel DGPad. (au besoin, utiliser la molette pour zoomer et le clic droit pour déplacer l’animation).

Troisième point
Bien que les élèves aient éprouvé des difficultés dans le travail sur support papier et qu’ainsi ils aient pu percevoir la complexité d’un pavage, ils n’ont par contre pas pu appréhender la prouesse que représente sa conception. Nous pourrions les faire travailler sur des fichiers Geogebra laissant davantage de liberté et de création.

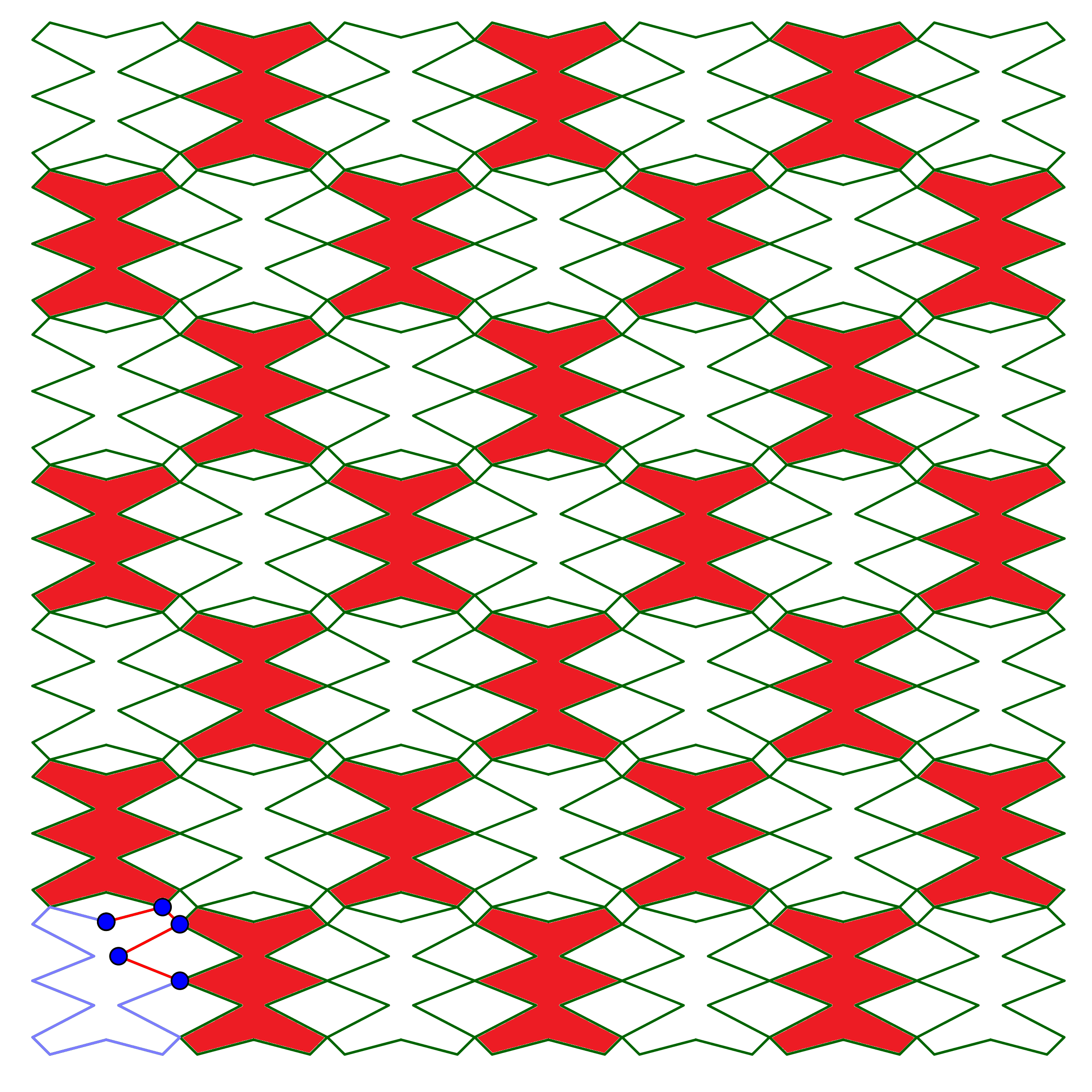
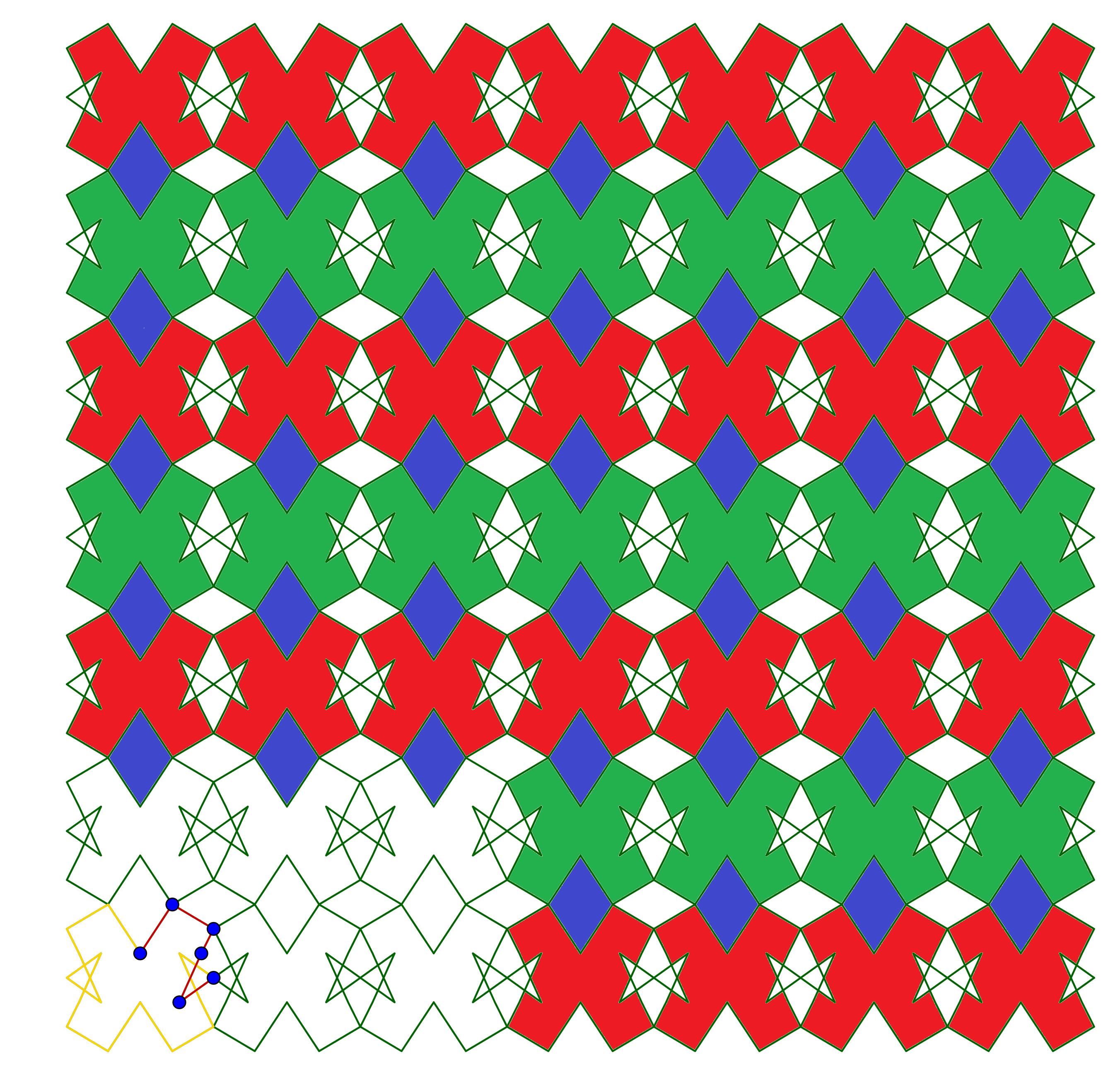
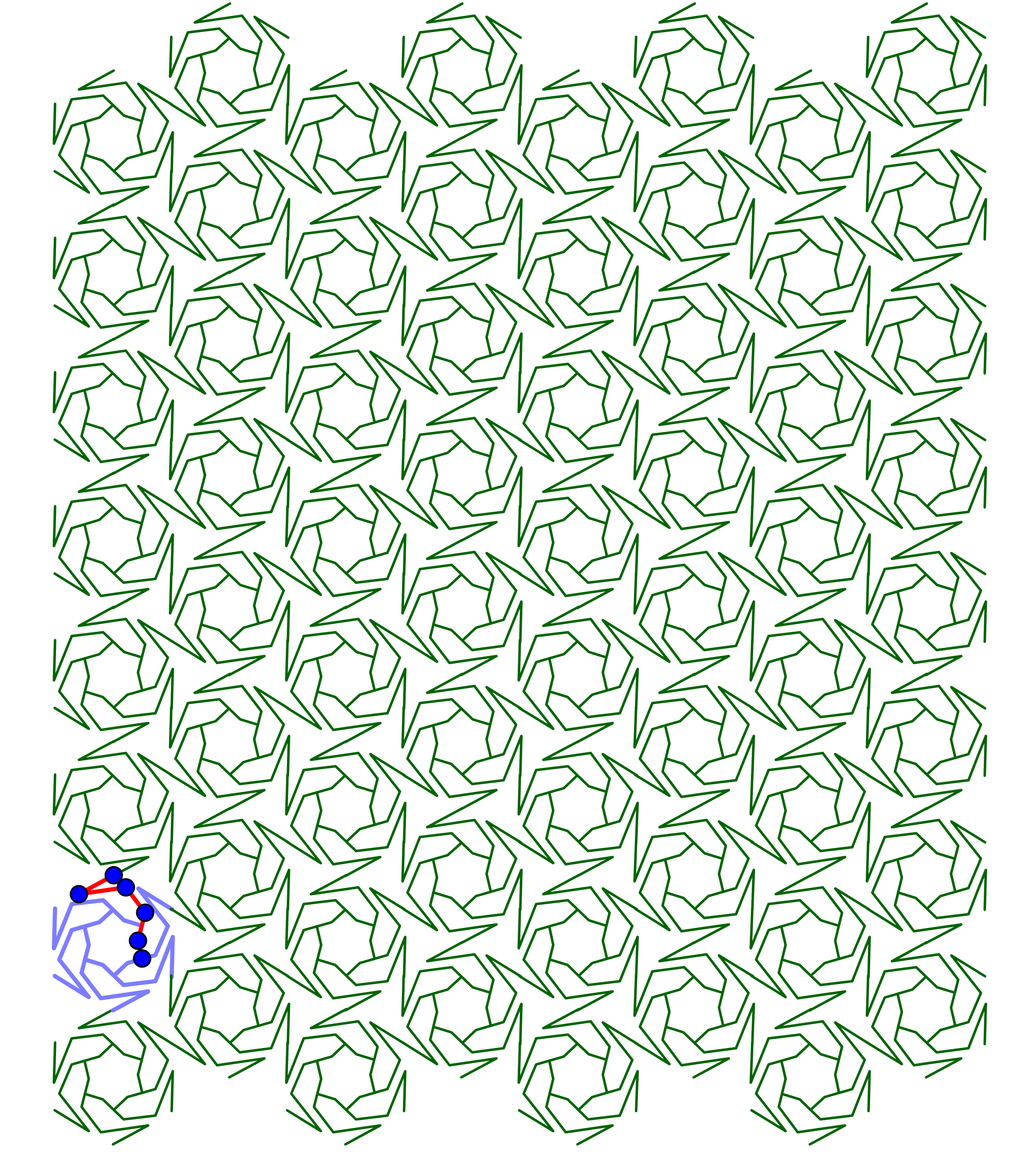
Les trois fichiers proposés ci-dessous permettent de manipuler le motif minimal en visualisant en temps réel l’effet sur le pavage (cliquez sur l’image pour ouvrir les fichiers Geogebra dans le navigateur) :

Nous pourrions demander aux élèves :

• de déterminer les transformations nécessaires au pavage du plan et dans quel ordre.
• de faire apparaître la figure usuelle la plus petite possible qui permet de paver le plan.
• de réaliser un pavage de type islamique, c’est-à dire, un pavage dans lequel aucune ligne n’est interrompue.

Pour une utilisation optimale, il ne faut pas hésiter à utiliser le zoom et éventuellement la grille de Geogebra pour placer les points parfaitement.

Quelques liens et livres

• Islamic Geométric Pattern, écrit par Eric Broug.
  C’est un livre dans lequel l’auteur explique la construction à la règle et au compas de pavages islamiques décorant certaines mosquées ou palais. Les illustrations sont très claires et pédagogiques, les règles artistiques et mathématiques qui rendent spécifiques ces pavages sont très bien explicitées. Pour compléter ou se faire une idée sur internet :
  • School of Islamic Geometric Design
  • Broug.com

• Culture :
  • La collection du Louvre
  • L’institut du monde arabe

• Une banque impressionnante de motifs : Pattern in Islamic Art

• Dans le domaine mathématique :
  • un article de l’APMEP : L’Alhambra et ses pavages
  • un article sur le site mathématique de l’académie de Nantes : frises et pavages
  • Un projet sur le site de l’IREM de la Réunion : Algorithme de classification des 17 pavages
  • un article très visuel sur les 17 pavages du plan par Thérèse Eveilleau : les 17 pavages du plan

Le projet 2017-2018

Quelques modifications et améliorations par rapport au projet originel

En mathématiques, le principal écueil rencontré l’année précédente était lié à la difficulté pour les élèves d’appréhender la notion de motif minimal dans le travail sur papier décrit dans la partie "Du pavage au motif minimal". De fait, il avait été nécessaire d’expliciter cette notion et les consignes entre les deux séances de travail en groupe, ce qui avait notoirement allongé la durée prévue pour ces travaux.
De plus, je regrettais personnellement de n’avoir pas su faire sentir aux élèves la virtuosité que représente la conception d’un pavage islamique.

Pour répondre à ces deux problématiques, un travail sur l’observation et la création par les élèves de pavages islamiques me semblait tout indiqué. Je l’avais d’ailleurs évoqué dans la partie précédente intitulée "évolutions possibles".
Ce travail a été placé avant la visite au Louvre et s’est poursuivis après la visite. C’est ce travail qui est décrit ci-dessous, le reste du projet ("La visite", "Du pavage au motif minimal", "Du motif minimal au pavage") étant identique.

En français, l’objectif final d’écriture du huitième voyage de Sindbâd par les élèves reste le même. Mais cette année, il s’articule autour de la conception et de l’utilisation d’un jeu de sept familles. Ce travail est plus amplement décrit dans la partie "Les productions liées au projet" ci-dessous.

Observation et création de pavage islamique

Préalablement à cette séquence d’enseignement, une présentation de 10 minutes est effectué en classe à partir du fichier suivant : exemple_pavage.pdf
L’objectif est de présenter rapidement ce qu’est un pavage islamique, qu’elle en sont les règles, et d’évoquer une première fois la recherche d’un motif minimal permettant le pavage.

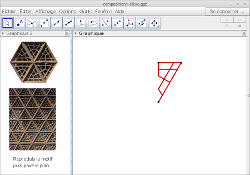
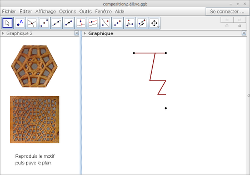
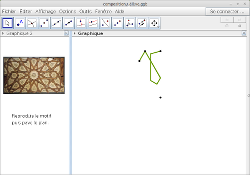
La suite du travail se déroule sur deux heures en salle informatique à partir des fichiers suivants (cliquez sur les images pour ouvrir les fichiers dans le navigateur) :

Les consignes données sont les suivantes :
1) Détermine les transformations qui sont nécessaires pour paver le plan à partir du motif de départ.
2) Quelle est la figure usuelle la plus simple qui permet de paver le plan sans qu’il y ait d’espace dans le pavage ?
3) Réalise un pavage islamique (tu enregistreras ton travail dans ton dossier personnel).

Pour les questions 1) et 2), les élèves répondent sur un formulaire en ligne ayant la forme de QCM.
La question 1) est assez ouverte et offre un éventail de réponses correctes assez variées. Il n’y a donc pas de réponse attendue, l’objectif principal de cette question étant de forcer l’élève à réfléchir aux manières d’obtenir la pavage à partir du motif minimal déplaçable et de réinvestir ses connaissances sur les transformations.
Pour la question 2) par contre, une rapide mise en commun en classe sera réalisée lorsque tous les élèves y auront répondu pour les trois pavages proposés.

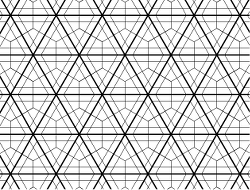
La question 3) porte l’objectif principal de la séquence, à savoir la création par les élèves d’un pavage islamique. Il est nécessaire de rappeler les caractéristiques d’un pavage islamique :
– les motifs sont tous joints (pas d’espace entre eux)
– les lignes ne sont jamais interrompues

Pour joindre les lignes et les motifs, il faut placer les points très précisément. L’utilisation du zoom de Géogebra est donc nécessaire.
Les créations d’élèves sont sauvegardées en image (.png) et colorisées avec un logiciel de retouche photo (ici Paint).

Après ces activités, la plupart des élèves ont une vision plus claire de la notion de motif minimal permettant le pavage.

Quelques travaux d’élèves

Pour chacun des trois types de pavage, les élèves ont réalisé des créations assez différentes et ont fait preuve de beaucoup d’imagination (cliquez sur les images pour les agrandir) :

Les productions liées au projet 2017-2018

Un livret a de nouveau été réalisé, regroupant l’ensemble des productions des élèves :

• Les textes réalisés en Français autour de Sindbad le marin.
• Les figures réalisées à l’aide de Geogebra autour des pavages : celles réalisées lors de la séquence "l’observation et la création de pavage" et celles réalisées lors de la séquence "Du motif minimal au pavage".

Quelques précisions concernant le travail en français
Conception d’un jeu des sept familles

Cette année, la classe a réalisé un jeu des sept familles à partir de Sindbâd de la mer, projet que je n’avais pas eu le temps de faire aboutir l’année précédente.

A la fin de la séquence, la conception du jeu amène les élèves à avoir un regard réflexif sur l’ensemble de l’œuvre étudiée. En effet pour définir les familles, ils doivent se mettre d’accord sur les sept thèmes les plus importants. Les élèves ont d’abord choisi ces sept thèmes en groupes. Puis un débat en classe entière a permis d’arriver au choix définitif : ce débat oblige les élèves à justifier leurs choix en revenant régulièrement au texte et en hiérarchisant les thématiques. Ensuite afin d’illustrer chacun de ces thèmes par six exemples, ils se sont replongés dans l’œuvre, alternant discussions, recours à la mémoire, lecture en diagonale. Là encore le débat en classe entière s’appuie sur des listes dressées auparavant en groupes.

Chaque carte devant être illustrée par un dessin, la réalisation matérielle du jeu sollicite les représentations mentales de chaque élève et amène à comparer comment chacun a visualisé les éléments clés choisis pour le jeu. De nouveau les discussions poussent les élèves à revenir au texte pour se mettre d’accord.

Le travail d’analyse mené pour la conception du jeu permet aux élèves de mieux comprendre les modalités d’écriture des sept voyages : comme beaucoup de contes, ceux-ci sont composés de reprises et de variations. Certaines créatures reviennent plusieurs fois, donnant son unité au récit : l’oiseau Rukhkh, le serpent géant, les géants... Certains épisodes aussi sont repris, mais avec suffisamment de variations pour éveiller la curiosité : l’exploration d’une nouvelle île, le naufrage, la découverte d’un peuple singulier, le sauvetage, la fuite par une rivière souterraine, les retrouvailles avec un équipage.

La conception du jeu sert ainsi de point d’appui pour l’écriture du huitième voyage que les élève réaliseront en groupe. En analysant les aventures de Sindbâd, ils comprennent que les récits ne naissent pas seulement du jaillissement de l’imaginaire. Écrire, c’est aussi s’inspirer d’autres textes, s’approprier une idée pour la transformer et la faire sienne. Cette prise de conscience permet de démystifier, de dédramatiser l’entrée dans l’écriture. Elle sert aussi à mettre en place des stratégies d’écritures : face à un sujet nouveau, face à la page blanche, il est utile de faire le point sur ce qu’il va être possible de reprendre des textes déjà lus ou déjà écrits. Pour concrétiser cette dimension de l’écriture, les élèves tirent au sort trois cartes du jeu des sept familles qu’ils devront utiliser dans leurs textes.

En conclusion, la conception du jeu des sept familles a nourri et dynamisé le travail d’analyse et d’écriture en donnant un objectif concret et ludique. Chaque élève a reçu en fin de séquence un jeu de quarante deux cartes rassemblant l’ensemble de leurs réalisations. Puis ils ont concrètement mis en pratique les théories de Catherine Tauveron sur la littérature comme jeu, en disputant des parties avec les cartes qu’ils avaient créées.

Jean-Baptiste Olin

Voici le jeu des sept familles créé par les élèves :

Retour d’expérimentation

En mathématiques, l’apport du travail sur l’observation et la création de pavages islamiques, a nettement amélioré la compréhension des élèves sur les pavages, sur la notion de motif minimal et a ainsi beaucoup fluidifié l’enchaînement des différentes séquences proposées.
Pour parfaire encore le projet, on pourrait imaginer davantage de fichiers à partir desquels les élèves créent le leur. Ceux-ci seraient construis sur d’autres types de pavage, améliorant encore la diversité des productions d’élèves.

_