Le calcul littéral est sûrement l’un des points les plus délicats des programmes de mathématiques au collège. On oublie facilement à quel point l’apparition de cette façon d’exprimer les problèmes et de les résoudre est récente dans l’histoire des mathématiques. Il nous semble qu’il n’est pas possible de "traiter le sujet" en deux ou trois semaines en classe de quatrième, quelle que soit la façon dont on s’y prenne. Un travail préparatoire s’impose depuis la classe de sixième, qui doit avoir deux objectifs :

– d’abord motiver l’introduction d’une variable en la proposant dans des situations où elle peut sembler commode, voire indispensable : élaboration de définitions, de conjectures, de théorèmes généraux sur les nombres, preuves simples en arithmétique, mais aussi dialogue avec la machine (programmation, tableur).

– ensuite fournir des occasions de travailler avec une variable. Lorsque la mise en équation de problèmes est prématurée (en 6ème et 5ème), l’informatique fournit de telles occasions.

Voici un exemple d’activité qui concerne les niveaux sixième-cinquième. Le principe peut être étendu au niveaux supérieurs en augmentant les exigences (un fichier pour les troisièmes est proposé en fin d’article).

Les élèves ont devant eux la feuille de calcul suivante :

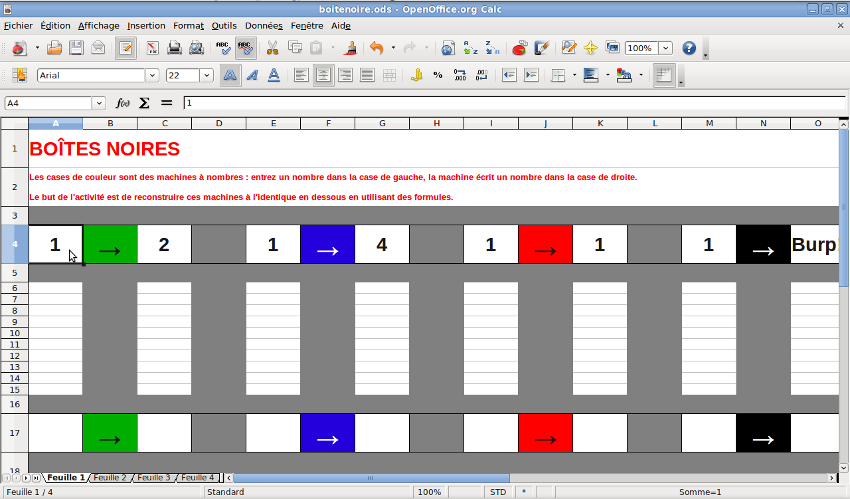
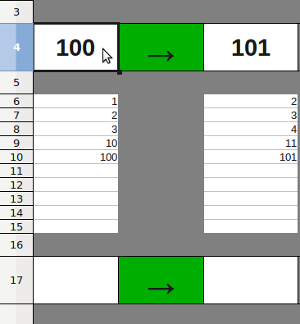
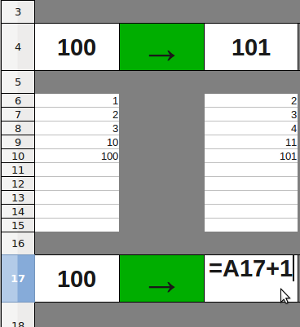
Ils peuvent entrer un nombre dans la case A4 : la case C4 se remplit automatiquement, mais la formule qui a servi à la remplir est cachée, seul le résultat du calcul s’affiche. Le but de l’activité est de reproduire cette "machine" à l’identique sur la ligne n°17 en utilisant une formule.

Quelques étapes du travail de l’élève :

Essais : l’élève teste la machine pour comprendre comment elle fonctionne. quelques cellules sont laissées à sa disposition pour noter ses essais successifs.

Écriture d’une formule : l’élève a compris ce que faisait la machine, il le traduit en langage de tableur.

Vérification : l’élève doit être capable de reconnaître que sa machine n’est pas identique au modèle en la testant sur des exemples. Si l’enseignant ne peut trouver d’exemple qui mette en défaut la formule de l’élève, celle-ci sera déclarée juste.

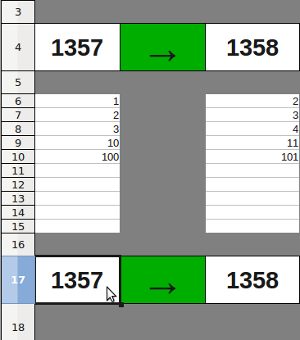
Remarques :

– S’il s’agit d’une toute première séance sur le tableur, l’enseignant devra peut-être commencer par un petit travail sur la désignation des cellules (notations A4, C17...). Mais rien n’empêche d’aborder le système des formules pour la première fois dans cette activité.

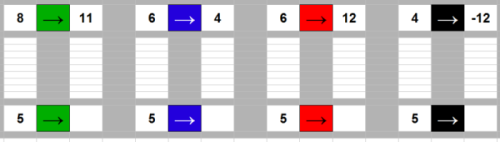
– Le stade où l’élève écrit des formules statiques du style "=3+1" semble être inévitable : c’est l’occasion de faire parler les élèves sur ce qu’ils entendent par "deux machines identiques", et de s’entendre sur une méthode de vérification.

– L’objectif principal de cette activité n’est pas tant que les élèves sachent décoder une machine compliquée, mais qu’ils aient compris ce qu’est une machine, c’est à dire : comment on crée une machine par le système des formules, et ce que sont deux machines identiques. Les quatre ou cinq premières machines proposées doivent être excessivement simples, pour que tous les élèves puissent y travailler et se familiariser avec le système des formules. Cependant, il est nécessaire de proposer rapidement des machines plus difficiles, car c’est le défi lancé à leur capacité de recherche qui motivera les élèves : cette activité ne doit surtout pas se contenter d’être un exercice de manipulation de notations. Les élèves de sixième et cinquième peuvent devenir très habiles à ce décodage, qui fait intensément travailler le calcul mental. On peut raisonnablement proposer toutes sortes de fonctions affines à coefficients entiers relatifs (en prenant quelques précautions en sixième), et même des polynômes du second degré.

– Après avoir mené cette activité suffisamment longtemps (deux séances au moins) devant les ordinateurs, le travail peut se prolonger en classe : l’enseignant peut proposer une machine à décoder en fournissant trois nombres et leurs images. Cela peut être l’occasion, en 5ème, d’approfondir un peu la notion de machine en constatant que deux machines peuvent coïncider sur deux (ou trois) valeurs sans être identiques, que plusieurs formules peuvent convenir pour une même machine (ce qui peut fournir une introduction à la distributivité par exemple)...

– Quelques exemples de fonctions à proposer :

• x-> 2x+1 peut être un premier exemple de fonction affine non triviale. En augmentant les coefficients, on fait travailler sur les multiples d’un entier, éventuellement sur la division euclidienne ;
• x-> 7(x+2)pourra donner lieu à deux formules valables différentes. En cinquième, cela pourra être exploité pour la distributivité.
• x-> 20-x est excellente pour travailler sur la soustraction. Les élèves sont très rapidement capables de prédire la sortie de la machine, mais ont souvent bien du mal à en tirer une formule.
• x-> x^2 , après plusieurs exemples affines, est un bon test pour savoir où en sont les élèves dans leur compréhension de ce qu’est la variable dans le tableur.

Ci-dessous, deux fichiers créés par le tableur d’OpenOffice. Le fichier "boitenoire.ods" est un exemple de fichier à donner aux élèves (addition et soustraction de nombres entiers en sixième). Les feuilles sont protégées par un mot de passe : "motdepasse". Le fichier "modele.ods" est un modèle de fichier vide de formules (pour la mise en page). Sous OpenOffice, les feuilles devront être protégées une à une par un mot de passe (tools->protect document->sheet)

Ci-dessous, un fichier pour le niveau 3è qui peut servir d’introduction à la notion de fonction.