Patron de pyramide et projeté du sommet
1. Activités papier : projeté du sommet
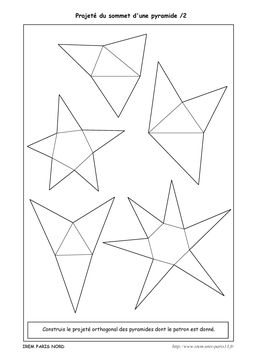
Les deux activités proposées ont pour but de faire constater aux élèves que l’on peut avoir une idée précise de la position du sommet d’une pyramide en déterminant la position de son projeté orthogonal sur son patron.
Le travail sur le projeté du sommet permet non seulement de résoudre davantage de problème de construction de patron de pyramide (voir les activités du 2)) mais permet à l’élève de faire davantage le lien entre le patron et le solide. Ce lien est représenté par le projeté qui est un point du patron et qui "représente" le sommet qui est un objet caractéristique du solide.
Il n’en va pas de même pour l’activité suivante où les bases sont désormais des polygones ayant un nombre impair de côtés (sauf pour un). L’élève devra donc généraliser ce qu’il a constaté dans la première activité pour pouvoir formuler le fait que le projeté se situe à l’intersection des droites perpendiculaires aux côtés de la base qui passe par les points du patron représentant le sommet de la pyramide.
2. Activités papier : application à la construction de patron
L’ensemble des activités proposées ne peuvent être résolues sans l’utilisation du projeté orthogonal du sommet.
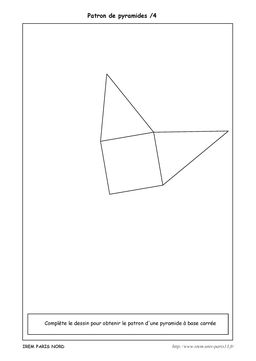
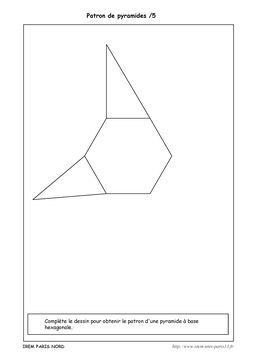
Dans cette 1ère série, il s’agit de compléter les figures afin qu’elles deviennent des patrons de pyramide.
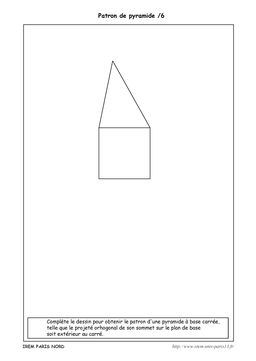
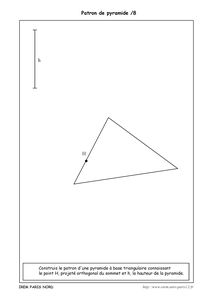
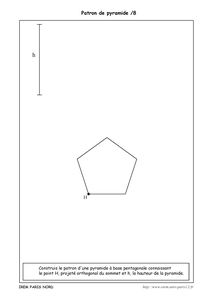
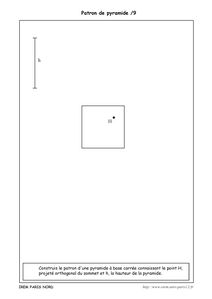
Dans cette deuxième série, on demande de construire le patron d’un pyramide connaissant la base et la position du projeté orthogonal du sommet sur celle-ci et la hauteur de la pyramide.
Pour les deux premières, il suffit de reporter la hauteur perpendiculairement au côté où se trouve le projeté du sommet. Ensuite, il suffit de compléter le patron.
Pour les suivantes, il faut tracer un triangle rectangle comme illustré ci-dessous :
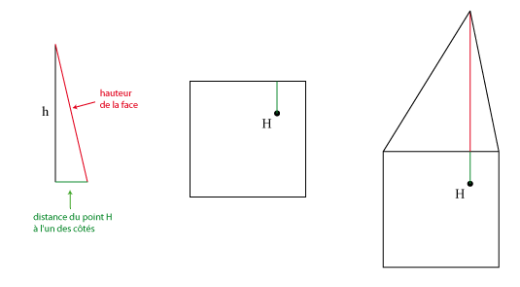
Le triangle que l’on trace est souvent utilisé lors des calculs de la hauteur de la pyramide. Ainsi, en travaillant ce type de construction, on donne une existence concrète à ce triangle et sans doute facilitons-nous la compréhension des élèves.