espace, cube, pavé droit, perspective, volume, compter
Construction de solides à partir de cubes
Les objectifs :
L’objectif de ce logiciel est de travailler le repérage dans l’espace, la vision dans l’espace, ainsi que la notion de volume en permettant à l’élève de construire des solides.
Ainsi, il devra utiliser celui-ci pour construire les solides et trouver leurs volumes mais devra progressivement s’en passer pour faire appel à des représentations mentales et à des raisonnements.
Cette activité fait partie des leçons de 6è sur la géométrie dans l’espace et peut servir d’accompagnement aux activités papier proposées dans le livre sur la géométrie dans l’espace "La troisième dimension".
On peut remplacer ce logiciel (qui peu à peu devient obsolète) par des activités utilisant GeoGebra. Pour cela, voir l’article : Visualiser dans l’espace pour calculer des volumes
Présentation et Installation :
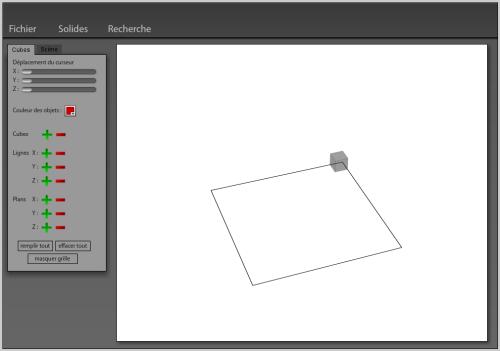
Le logiciel est un programme flash. Cliquez sur l’image pour accéder à ce programme.
Pour installer ce programme sur un poste en local (multi-plateformes), une version AIR est disponible. Cette version à l’avantage d’être plus rapide que la version sur internet, d’éviter les problèmes de connexion et de pouvoir la garder en archive chez soi. (obsolète, adobe air n’étant plus maintenu. La version dans le navigateur marche encore actuellement.)
Pour l’installation, il faut suivre cette démarche :
-
Télécharger et installer l’environnement Adobe Air en suivant ce lien. -
Télécharger le fichier "Comptage_cube_air.air" en suivant ce lien, puis double-cliquez dessus pour commencer l’installation.
Il est possible de vérifier si des mises à jour sont disponibles avec une connexion internet dans le menu "Rechercher".
Utilisation du programme flash
il y a 3 menus distincts :
- Fichier : permet d’ouvrir, enregistrer les solides et exporter une image de la scène. En accès professeur, l’enregistrement permet d’accéder à d’autres paramètres de configuration. Il pourront être modifiés par la suite via l’onglet "modifier les paramètres".
- Solides : permet d’accéder à une série de solides préconfigurés.
- Recherche : permet de rechercher d’autres solides sur le site de l’IREM, de proposer des solides par envoi par mail...
Les barres d’outils :
- par défaut apparaît les différents outils qui permettent de construire le solide et de configurer la scène. Ils sont assez intuitif, il suffit d’essayer pour comprendre leur fonctionnement.
- Dans le cas de l’ouverture d’un solide comme modèle, une boîte apparaît permettant à l’élève de voir l’énoncé et de saisir une réponse.
La configuration des modèles se fait lors de l’enregistrement du solide en mode professeur. Il suffit de remplir les champs de saisie, de décocher le bouton "solide visible sur la scène" et de cocher le bouton "miniature comme modèle".
Détail du menu "solides" :
La progression des solides est volontaire mais peut être changée.
L’élève travaille sur l’outil informatique en utilisant le menu "Solides" et dispose d’une feuille de papier sur laquelle il notera les procédures de calcul qui lui ont permis de calculer les volume des différents solides.
D’autres solides sont disponibles dans le menu "Rechercher". Vous pouvez aussi les visualiser ici.
- solide1 et solide 2 :


|
Ces deux premières figures permettent à l’élève de se familiariser avec la construction de solide. Il n’est pas si évident de se repérer dans cet environnement. En effet, pour réaliser ces solides, il doit comprendre qu’il lui faut procéder par empilement de proche en proche et choisir des repères stables : par exemple, la face représentant le sol. Sans cela, un cube visible peut correspondre à plusieurs autres cubes ayant des cordonnées différentes. |
- solide 3 :

|
Ce solide est un cube 5*5*5 auquel on a enlevé les 8 cubes à chaque sommet. La procédure attendue est de calculer le volume du cube puis d’enlever le volume des 8 petits cubes. Lors de la construction du solide, l’élève peut découvrir par dénombrement le volume du cube. Puis avec l’obligation d’écrire un calcul, il devra chercher à généraliser et trouver "la formule" permettant le calcul. Pour les élèves ayant des difficultés à démarrer ou à construire le solide, on peut leur demander de procéder par étapes : d’abord, on peut leur demander de construire la rangée de cubes posée sur le sol, enlever les cubes en trop, puis la rangée supérieure et ainsi de suite... jusqu’à ce qu’il réalise de lui-même l’existence de procédures plus simples. |
- solide 4 :

|
Ce solide est entouré d’un ruban. L’élève doit trouver l’aire coloriée en vert. La procédure attendue est de calculer l’aire totale du cube puis de lui soustraire l’aire du ruban rouge. Le but de ce problème est de permettre à l’élève de faire la différence entre le volume d’un solide et l’aire de ses faces. |
- solide 5 :

|
Ce solide est un cube 8*8*8 auquel on a enlevé un pavé 4*4*7. La procédure attendue est donc de calculer le volume du cube, celui du pavé puis d’en faire la différence. L’élève devra s’interroger sur la procédure permettant le calcul du volume du pavé (avec toujours la possibilité de construire et de dénombrer). |
- solide 6 :

|
Ce solide est un pavé 8*6*5 auquel on a enlevé un cube 2*2*2 et 3*3*3. La procédure attendue est évidente. |
- solide 7 :

|
Un cube vert 9*9*9 est traversé par un solide rouge rappelant la forme d’un prisme à base triangulaire. On demande le volume du solide vert. L’élève doit s’interroger sur la manière de calculer le volume du solide rouge. Lorsqu’un élève est bloqué, on peut lui demander de construire ce solide. L’utilisation de l’outil "rangée" est alors très efficace et peut aider l’élève à découvrir la procédure de calcul : nombre de cubes dans une rangée * nombre de rangée. |
- solide 8 :

|
Ce solide est un pavé 8*8*4 auquel on a enlevé quatre pavés 4*2*2. |
- solide 9 :

|
Un cube 10*10*10 est formé de deux solides identiques en forme de "L" et d’un pavé 10*6*4 qui le traverse de par en par. La procédure attendue est : (10*10*10-10*6*4)/2. |
- solide 10 :

|
Ce solide à l’allure d’un paquet cadeau. C’est un cube vert 7*7*7 entouré de rubans rouges. On demande de calculer l’aire verte. La procédure experte est de calculer l’aire totale du cube (4*7*7) et d’y enlever l’aire coloriée en rouge (6*13). Ce problème est l’occasion de bien des débats quant à la manière de procéder. |