Sommaire

• Présentation des fichiers
• Démarches et utilisation
• Progression et résultats attendus
• Pour aller plus loin

Présentation des fichiers

Tous les fichiers de cette série fonctionnent de la même manière et s’adressent principalement aux élèves de fin de cycle 3. Un solide manipulable est proposé. Il faut déterminer le nombre de sommets, de faces et d’arêtes du solide. L’élève peut saisir ses réponses qui seront validées (vert) ou invalidées (rouge).

Pour faire un travail plus approfondi, il est possible de demander la nature des faces de chaque solide. Par contre, il n’y a pas de vérification automatisée.

La zone de saisie étant une zone de calcul formel, l’élève peut saisir des suites de calculs organisés sur une ligne.

Les objectifs de cette séquence sont multiples :

• Travailler la vision dans l’espace :
  • Voir ce qui est caché.
  • Travailler sur la nature des faces
  • Comprendre que la vue d’une face est déformée par la perspective sauf lorsqu’on la voit de face.
• Travailler sur le vocabulaire nécessaire à la description d’un solide.
• Organiser un dénombrement.
• Gérer l’hétérogénéité en proposant des activités de recherche à la fin de la série.

Par exemple, l’activité "Un tétrakaidécaèdre" accessible ici, se présente de la manière suivante (Cliquez pour voir l’image en grand) :

La réponse attendue ici est :
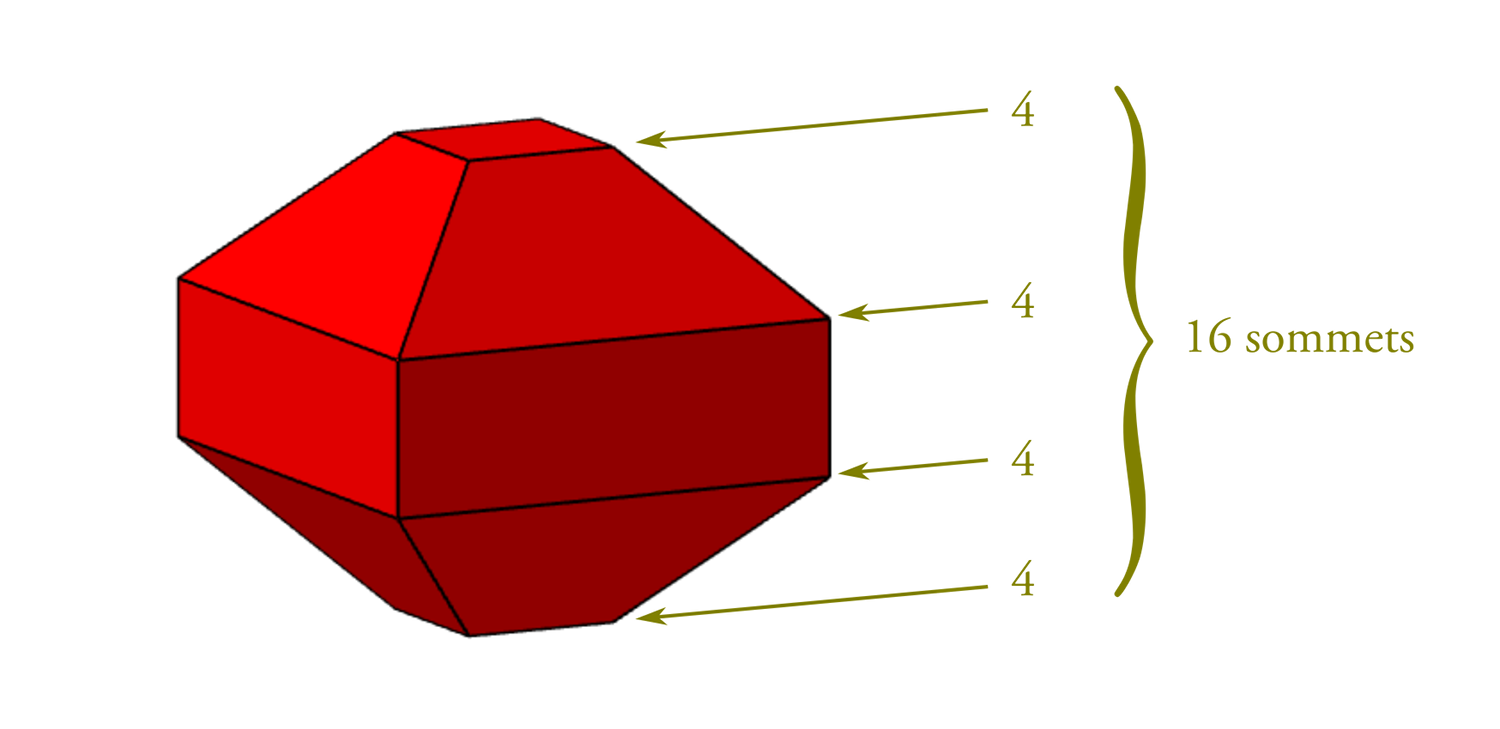
– Sommet = 16
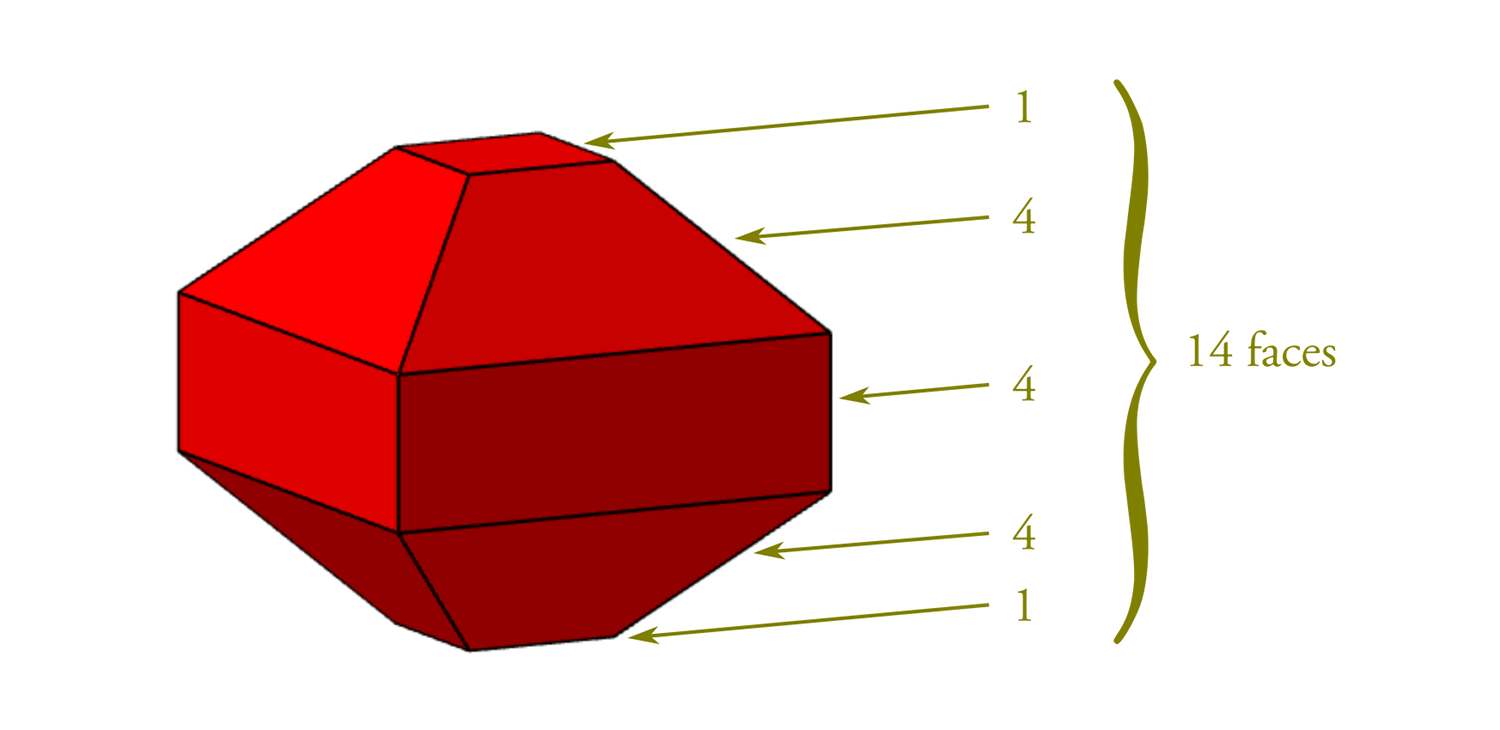
– Faces = 14 (dont 2 carrés, 4 rectangles et 8 trapèzes isocèles)
– Arêtes = 28

Démarches et utilisations

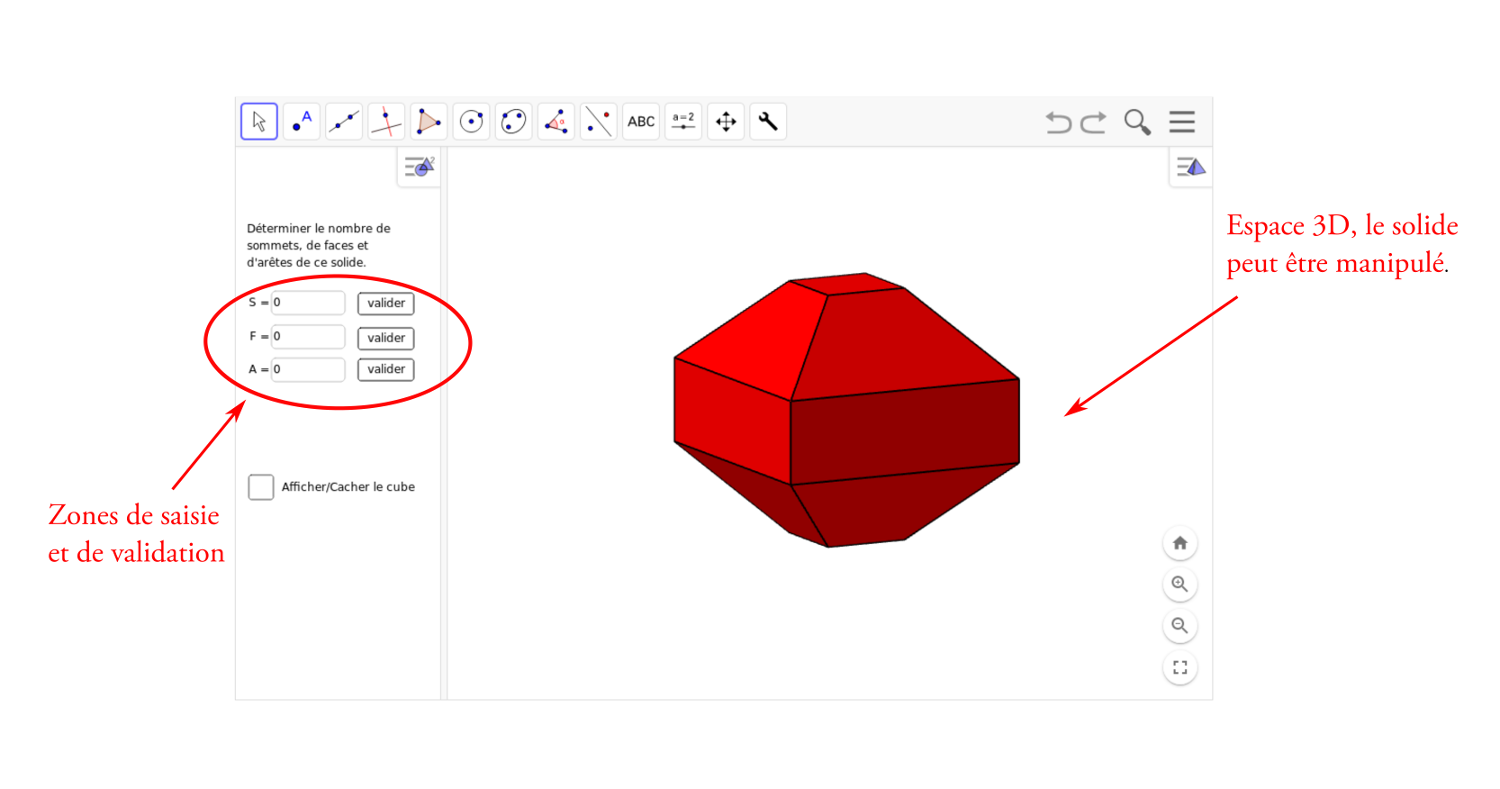
Déterminer le nombre de sommets, de faces et d’arêtes d’un solide nécessitent de la part de l’élève une représentation mentale claire de celui-ci. En effet, le comptage s’opérant la plupart du temps à partir d’une vue fixe du solide, l’élève doit voir, imaginer ce qui est caché. Le fait qu’il puisse manipuler le solide à sa guise permet de construire cette représentation.

La difficulté croissante des solides proposés oblige rapidement l’élève à passer d’un comptage empirique de un en un, à un comptage expert à base de calcul. Il lui faut de plus prendre des points de repère : la plupart du temps, il s’organise pour compter du haut vers le bas.

Ainsi, pour le tétrakaidécaèdre, le comptage peut prendre cette forme :

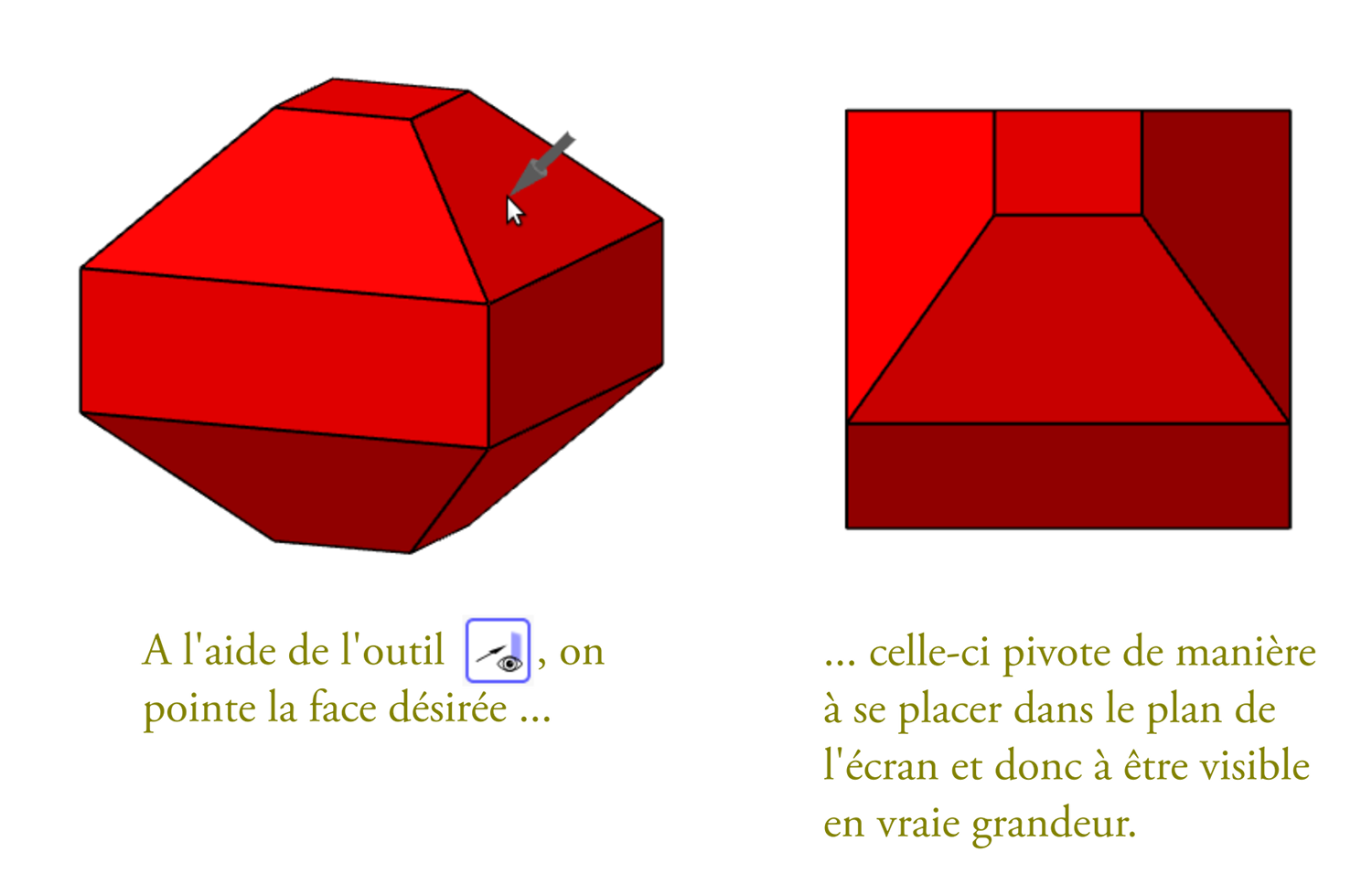
Le travail sur la nature des faces vise à compléter la représentation mentale du solide. Il permet de faire prendre conscience de manière sensible à l’élève que la représentation dans l’espace déforme sauf lorsque l’on place la figure souhaitée dans une vue de face.
Comme il peut être parfois difficile de faire une vue de face précise seulement en manipulant l’espace graphique, l’outil "vue de face" de Géogebra peut être utile. Son utilisation est illustrée ci-dessous :

Cette série d’activités peut être utilisée collectivement en classe (dans ce cas, c’est l’enseignant qui manipule l’espace 3d) ou bien de manière individuelle sur un support numérique (tablette, PC en salle informatique ...) que ce soit en classe ou à la maison. Dans ce dernier cas, Il peut être pertinent de demander une trace écrite aux élèves afin de voir leur progression. En effet, sans trace écrite, il peut être difficile d’évaluer ce qui a été fait ou pas par l’élève, dans quel ordre, s’il a réfléchi aux natures des faces ...

Ces deux manières d’utiliser les activités peuvent évidemment être menées conjointement.

Progression et résultats attendus

La progression proposée sur Rubricamaths est basée sur une complexification progressive des solides que se soit en terme de nombre de sommets ou que se soit en terme de difficulté à voir. En effet, certains solides sont faciles à percevoir car ils offrent des points de repère évidents même avec de nombreux sommets (les prismes ou les pyramides). D’autres sont plus difficiles à percevoir alors qu’ils ne présentent pas un nombre de sommets très importants (le dodécaèdre rhombique). Quelques solides très difficiles sont proposés à la fin de la série pour gérer les élèves en avance (à partir de l’icosaèdre tronqué). Les tous derniers sont à priori infaisables (surtout concernant le nombre d’arête) mais ils sont une source d’émerveillement et de curiosité qu’il serait dommage de ne pas leur faire partager.

Ci-dessous, les réponses attendues pour chacune des activités :

Quelques éléments de classification des solides

On retrouve dans les solides proposés :

1) Les cinq solides de Platon (polyèdres réguliers)

• le tétraèdre régulier
• le cube
• l’octaèdre régulier
• le dodécaèdre régulier
• l’icosaèdre régulier

2) Les treize solides d’Archimède (polyèdres semi-réguliers autres que les polyèdres réguliers, les prismes et les antiprismes)

• le tétraèdre tronqué
• le cube tronqué
• l’octaèdre tronqué
• le cubeoctaèdre
• le rhombicubeoctaèdre
• le cubeoctaèdre tronqué
• le cube adouci
• le dodécaèdre tronqué
• l’icosaèdre tronqué
• l’icosidodécaèdre
• le rhombicosidodécaèdre
• l’icosidodécaèdre tronqué
• le dodécaèdre adouci

3) Les solides de Catalan (duaux des solides d’Archimède)

• le triaki-tétraèdre (dual du tétraèdre tronqué)
• le triaki-octaèdre (dual du cube tronqué)
• le tétraki-hexaèdre (dual de l’octaèdre tronqué)
• le dodécaèdre rhombique (dual du cubeoctaèdre)
• L’icositétraèdre trapézoïdal (dual du rhombicuboctaèdre)
• l’hexaki-octaèdre (dual du cuboctaèdre tronqué)
• l’icositétraèdre pentagonal (dual du cube adouci)
• le triaki-icosaèdre (dual su dodécaèdre tronqué)
• le pentaki-dodécaèdre (dual de l’icosaèdre tronqué)
• le triacontaèdre rhomique (dual de l’icositétraèdre)
• l’hexacontaèdre trapézoïdal (dual du rhombicosidodécaèdre)
• l’hexaki-icosaèdre (dual de l’icosidodécaèdre tronqué)
• l’hexacontaèdre pentagonal (dual du dodécaèdre adouci)

4) Quelques solides des types suivants :

• prismes
• antiprismes
• pyramides
• bipyramides

Pour des informations plus exhaustives, le site Mathscurve est une référence.