L’objectif est de travailler le sens des opérations et d’initier à l’écriture de formules sans variable par le biais d’activités mentales ritualisées.

Des énoncés courts et simples contenant des nombres, suivis d’une question, sont dits oralement deux fois devant la classe. Ils sont donnés par série de deux ou trois. Les élèves répondent par écrit sur leur cahier et une correction est réalisée immédiatement après la série, voire après chaque phrase.

Ce type d’activité est proposé en série. Voici deux exemples de séquences :

La consigne donnée aux élèves est d’écrire la suite d’opérations sur une seule ligne conduisant à la réponse au problème mais sans en donner le résultat. L’élève est laissé libre d’utiliser le nombre de parenthèses lui semblant nécessaire à la compréhension de son expression.

Cette consigne est conforme aux attendus d’une fin de cycle 3, comme rappelé dans le document ressource sur le calcul en ligne au cycle 3 disponible sur Eduscol :

En fin de cycle, on tend progressivement vers un calcul organisé en une seule ligne, utilisant si
nécessaire des parenthèses. La capacité à écrire de telles expressions numériques prépare les
attendus du cycle 4 liés à la production d’expressions littérales et à la mise en équation de
problèmes.

http://cache.media.eduscol.education.fr/file/Nombres_et_calculs/00/2/RA_16_C3_MATH_calcul_ligne_c3_N.D_601002.pdf

Prenons comme exemple l’énoncé suivant :

J’ai 12 sacs de billes. A l’intérieur de chaque sac, il y a 5 billes rouges et 3 billes bleues.
Combien ai-je de billes ?

La réponse attendue sera : 12 x (5 + 3) ou (12 x 5) + (12 x 3)

Bien sûr d’autres réponses peuvent apparaître :

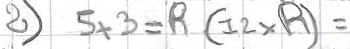
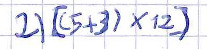
Il s’agira de laisser ce type de réponses émerger et de les faire évoluer vers l’écriture sur une seule ligne en proposant des énoncés du même type mais plus complexes. Pour cela, les énoncés peuvent être donnés avec des nombres qui rendent difficile le calcul mental ou avec une densité d’information plus importante .

Ainsi l’énoncé précédent peut être transformé de la manière suivante :

J’ai 17 sacs de billes. A l’intérieur de chaque sac, il y a 18 billes rouges et 16 billes bleues.
Combien ai-je de billes ?

Ou bien de la manière suivante :

J’ai 12 sacs de billes. A l’intérieur de chaque sac, il y a 5 billes rouges, 3 billes bleues, 6 billes vertes et 7 billes jaunes.
Combien ai-je de billes ?

Il n’apparait pas raisonnable de demander le résultat de ces problèmes en moins de 30 secondes, par contre, l’écriture sur une ligne n’est guère plus compliquée à produire que lors de l’énoncé initial. Écrire sur une seule ligne peut aussi permettre d’alléger la résolution du problème. En effet, en dégageant l’élève de la contrainte d’effectuer les opérations, celui-ci peut se concentrer sur la structure du problème.

Dans l’exemple suivant :

Une pile de 5 dictionnaires identiques pèse 17,2kg.
Combien pèserait une pile de 20 dictionnaires ?

La réponse attendue sera : (17,2 : 5) x 20

L’expression conduisant à la solution est nettement plus facile à produire que le résultat lui-même à cause de la difficulté d’effectuer la division décimale.

Les avantages de ce type d’activités nous ont semblé nombreux :

• la ritualisation permet d’enrichir le bestiaire mathématique des élèves, de leur rendre familières les formules sans variable.
• le temps très bref et le fait que les réponses soient apportées immédiatement permet d’apporter le retour immédiat dont le cerveau a besoin pour prendre conscience d’une erreur.
• il est relativement facile d’identifier le type de problèmes posant difficultés. On peut alors faire une séance plus spécifique sur ceux-ci.
• le temps de préparation de ce genre de rituel est quasi-nul, les phrases pouvant facilement être improvisées sur-le-champ par l’enseignant, puisant dans le quotidien de la classe ou l’actualité.
• l’oralité et le temps court en font un excellent exercice de concentration ou de prise de notes rapides.
• l’écriture d’une expression sur une seule ligne représente un enjeu mathématique important pour la suite (l’apprentissage de la notion de variable, de calcul littéral est basé sur ce type d’écriture)

Les objectifs mathématiques qui se cachent derrière chaque phrase sont si riches (priorités de calcul, distributivité, ...) que le professeur devra parfois se faire violence pour ne pas rebondir sur toutes les remarques d’élèves et risquer de dépasser les 10 ou 15 minutes de ce rituel. La répétition est une assurance que ces questions émergeront à nouveau.

La première difficulté de ce type d’activités réside dans la compréhension de la consigne : un problème sans réponse chiffrée peut être perçu comme un problème non résolu (par l’élève mais aussi par l’enseignant). En effet, l’élève ne pourra pas évaluer la pertinence de ses calculs par l’analyse du résultat obtenu. Pour pallier cet inconvénient, on peut proposer de réaliser ces problèmes à l’aide d’une calculatrice de type collège, en demandant aux élèves de saisir sur celle-ci une expression conduisant au résultat et en n’autorisant qu’une seule fois l’utilisation de la touche « = ».

Voici quelques captures d’écran de calculatrice :

On peu aussi énoncer la consigne de la façon suivante : "Vous devez écrire les calculs qui permettent de répondre à la question, mais il est interdit d’écrire un nombre qui n’est pas dans l’énoncé."

Faire varier les thèmes à l’infini est très intéressant pour la construction chez les élèves de catégories abstraites "addition", "multiplication", voire d’autres plus complexes. Après que le professeur aura lui-même fait varier les thèmes, il peut demander aux élèves de lui proposer leurs propres "micro-problèmes", avec la réponse.

Dans le même but, on peut proposer une variante, après un temps d’installation du rituel : le professeur ne dira plus la phrase, mais donnera la réponse, par exemple "3x5+2", et les élèves devront proposer une phrase qui lui corresponde.

Voici ci-dessous quelques exemples de micro-problèmes dans lesquels le professeur a fait varier les thèmes, puis ceux que les élèves lui ont envoyés.