L’introduction et la manipulation d’une variable est sans conteste un des écueils des programmes de mathématiques du collège et du lycée. Il convient d’y donner du sens, et il y a de nombreuses façons de le faire. Nous en décrivons une ici que nous avons choisi de présenter comme une séquence d’activités "rapides", en guise de rituel de début de séance, et qui peuvent facilement se décliner sur toute l’année scolaire.

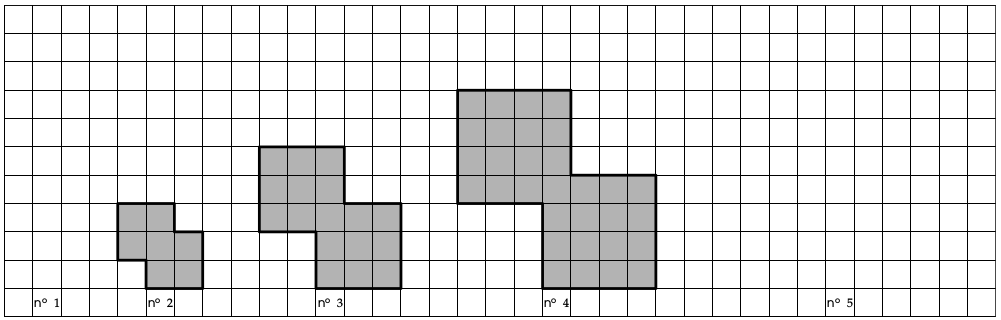
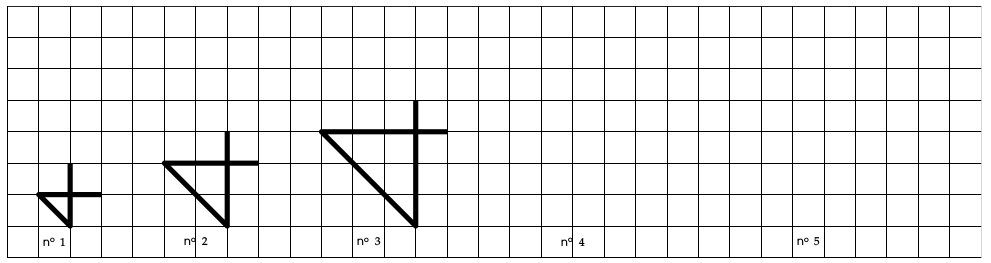
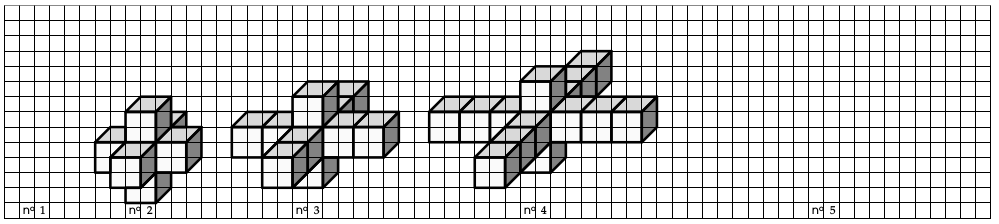
Cela peut par exemple se dérouler comme ceci : le professeur projette (ou imprime et distribue) l’énoncé, qui se présente comme une suite de figures numérotées.

Il pose alors une question (ou deux), qui sont du type :

- Dessinez les figures manquantes.
- Quelle est l’aire de la figure n°10 ? (n°100 ? n°2018 ?)
- Quelle est l’aire de la figure numéro N ?
- Idem pour le périmètre, le diamètre ou le volume.
- L’aire de la figure est-elle proportionnelle à son numéro ? (idem avec périmètre et volume)

Les élèves ont alors cinq ou dix minutes pour chercher une réponse. Ce temps écoulé, le professeur peut par exemple faire un rapide sondage sur les réponses trouvées et faire expliquer leur démarche par un ou deux élèves.

Certains élèves feront appel à des méthodes géométriques, comme un découpage des figures en éléments simples, d’autres (plus nombreux) leur préféreront systématiquement des méthodes numériques, fondées sur la seule observation des premiers termes de la suite numérique. La plupart d’entre eux trouvent rapidement une relation de récurrence, surtout si l’on prend soin de ne proposer au début que des suites arithmétiques. Survient alors un obstacle : la récurrence ne permet pas simplement de répondre à la question sur le n°100. Si la figure n°10 peut encore être dessinée, concrètement ou mentalement, la figure n°100 incite plutôt à un calcul mental qui reste parfois inconscient, certains élèves ayant une réponse sans toujours savoir de quel calcul elle découle, tandis qu’un élève qui donne la bonne réponse pour la figure n°2018 n’est plus très loin de pouvoir produire une formule avec une variable. D’autre part, poser l’une après l’autre les deux questions sur la figure n°10 puis sur la figure n°100, c’est inviter très lourdement à utiliser, le plus souvent à tort, la proportionnalité : cela peut être une volonté de l’enseignant. Au début, on verra parfois les élèves s’emparer de la variable « n° » ou « n°N » au lieu du « N » attendu. Les élèves les plus en difficulté n’accéderont pas tout de suite à la variable, c’est pourquoi une première question peut être nécessaire, mais ils peuvent toujours être actifs : les calculs d’aires et de volumes sur les premiers éléments de la suite ne sont pas hors de portée, et la reproduction des premiers motifs et des suivants est souvent très abordable même si elle n’est pas toujours triviale. Elle n’est pas inutile non plus : elle met sur la voie d’une méthode géométrique. Ces questions sont de jolis prétextes à parler de proportionnalité, en particulier d’exhiber des exemples de non-proportionnalité. Elles peuvent aussi faire parler d’agrandissements géométriques et de manipulations algébriques, les formules étant trouvées tantôt sous leur forme factorisée, tantôt sous leur forme développée. La difficulté pourra être, pour l’enseignant, de résister à la tentation de rebondir et de faire durer l’activité trop longtemps.

Vous trouverez dans le document pdf ci-dessous quelques exemples d’activités de ce type, mais cela peut se décliner à l’infini, et pour chaque suite de figures la liste des questions à poser n’est pas fermée. Nous avons fait le choix de ne pas écrire la consigne, de façon à laisser l’enseignant libre de la choisir. Il faudra juste être attentif à ne pas poser une question inaccessible, par exemple pour des sixièmes une question qui impose de connaître la longueur de la diagonale du carré de côté 1. Il est par ailleurs possible de demander aux élèves eux-mêmes de se poser une question au sujet d’une suite de figures.

Nous avons adapté cette série d’activités pour un usage en salle informatique : les élèves disposent d’un curseur pour faire varier la variable et doivent remplir un tableau qui est auto-correctif. L’usage de formules de tableur est possible dans GeoGebra, de sorte que les élèves qui ont compris la relation de récurrence peuvent remplir très rapidement les dix premières lignes du tableau : c’est l’occasion de leur montrer comment copier une formule vers le bas dans un tableur.

Vous trouverez ces activités autour les variables discrètes sur Rubricamaths dans la section "Fonctions, variables...".